
El Muestreo de Thompson y BayesUCB son dos algoritmos basados en ideas bayesianas con los que es posible obtener buenos rendimiento en problemas tipo Bandido Multibrazo.
Muestreo de Thompson
Uno de los algoritmos más antiguos que se utilizan para seleccionar los bandidos en problemas tipo bandido multibrazo es el Muestreo de Thompson ("Thompson Sampling"). Siendo un algoritmo probabilístico basado en ideas bayesianas. Se le llama "muestreo" porque para seleccionar el bandido toma una muestra aleatoria de distribución de probabilidad asociadas a cada uno de los bandidos. En el caso de que la recompensa se distribuya en base a una distribución Binomial se puede utilizar la distribución beta que es su conjugada.
Así, a cada uno de los bandidos se le asocia una distribución Beta donde los parámetros se obtienen mediante
\begin{aligned} \alpha &= \sum_i X_i \\ \beta &= \sum_i N_i - \sum_i X_i \end{aligned}
donde X_j son las recompensas obtenidas por el bandido j en cada una de las tiradas y N_j es el número de sucesos de la distribución Binomial. De modo que para seleccionar el bandido en cada una de las tiradas se obtendría una muestra de cada una de las distribuciones y se seleccionara aquella con mayor probabilidad.
Funcionamiento del Muestreo de Thompson
El Muestreo de Thompson no crea un mecanismo para resolver el problema, sino que asocia una distribución de probabilidad a cada uno de los bandidos. Distribución que se puede usar para estimar los resultados originales. A medida que aumenta el número de veces que se ha jugado con cada uno de los bandidos, la forma de las distribuciones se irá haciendo más estrechas en torno a la media. Por lo que, al obtener una muestra de cada una de las distribuciones es más probable que esta se encuentre cerca del valor esperado para ese bandido.
Recompensas arbitrarias
Anteriormente se ha asumido que las recompensas se obtienen mediante una distribución Binomial, lo que nos permite justificar el uso de la distribución Beta. En el caso de que no se conozca la distribución de las recompensas se puede emplear la distribución Gaussiana para realizar el muestreo y seleccionar el bandido. En este caso los parámetros se pueden obtener a través de las siguientes expresiones
\begin{aligned} \mu_j &= \hat{X_j} \\ \sigma_j &= \frac{1}{n_j + 1} \end{aligned}
Donde \hat{X_j} es la media observada en el bandido y n_j son las veces que se ha jugado con el bandido j.
BayesUCB
En la implementación UCB1 no se ha asumido que las recompensa provengan de ninguna distribución. Por lo que se usó la desigualdad de Hoeffding para obtener una estimación generalizada del intervalo de confianza. En el caso de conocer cuál es la distribución se podría obtener el intervalo de confianza de una manera más precisa. Así, basándonos en lo que hemos visto para el Muestreo de Thompson, se puede asumir que la distribución Beta para recompensas Binomiales y emplear como criterio de confianza una cantidad de distribuciones estándar para seleccionar el bandido. Esto es de puede usar la expresión para obtener UCB un Bayesiano
X_{Bayes-UCB} = \bar{X_j} + \gamma B_{std}(\alpha, \beta),
donde \alpha y \beta se calcula tal como se ha explicado anteriormente, \gamma es un hiperparámetro con el que se indica cuántas desviaciones estándar queremos para el nivel de confianza y B_{std} es la desviación estándar de la la distribución Beta con esos parámetros.
Si asumimos que la media de las distribuciones Beta es
\bar{X_j} = \frac{\alpha_j}{\alpha_j + \beta_j},
también se puede reescribir las expresiones como
X_{Bayes-UCB} = \frac{\alpha_j}{\alpha_j + \beta_j} + \gamma B_{std}(\alpha, \beta).
Implementación en Python
La implementación del Muestreo de Thompson se puede basar en la clase Epsilon se ha implementado anteriormente en la entrada de Epsilon-Greedy. En este caso es necesario modificar el constructor para tener en cuenta el nuevo parámetro y los métodos run(), select() y reset(). Clase que se muestra a continuación
from scipy.stats import beta
class ThompsonSampling(Epsilon):
def __init__(self, bandits, N=1):
self.bandits = bandits
self.N = N
self.reset()
def run(self, episodes=1):
for i in range(episodes):
# Selección del bandido
bandit = self.select()
# Obtención de una nueva recompensa
reward = bandits[bandit].pull()
# Agregación de la recompensa al listado
self._rewards.append(reward)
# Actualización de la media
self._plays[bandit] += 1
self._mean[bandit] = (1 - 1.0/self._plays[bandit]) * self._mean[bandit] \
+ 1.0/self._plays[bandit] * reward
# Guardado de valores intermedos
self._alpha[bandit] += reward
self._beta[bandit] += (self.N - reward)
def select(self):
num_bandits = len(self.bandits)
bayes = [0] * num_bandits
for i in range(num_bandits):
bayes[i] = beta.rvs(self._alpha[i], self._beta[i])
max_bandits = np.where(bayes == np.max(bayes))[0]
bandit = np.random.choice(max_bandits)
return bandit
def reset(self, initial=None):
self._rewards = []
self._plays = [0] * len(self.bandits)
self._mean = [0] * len(self.bandits)
self._alpha = [1] * len(self.bandits)
self._beta = [1] * len(self.bandits)
Como se puede ver en el código en los métodos run() y reset() incluye el cálculo y la inicialización de los dos parámetros de la distribución Beta. Al igual que en otras ocasiones, los cambios más importantes se encuentran en el método select(). En el que ahora se obtiene una muestra aleatoria para cada uno de los bandidos y se selecciona aquella con el valor más alto.
La clase ThompsonSampling se puede utilizar para implementar el método BayesUCB. Simplemente se tiene que cambiar el método select() de la clase para que la selección de base en el intervalo de confinada y no en el muestreo de los datos. Lo que se muestra en el siguiente código.
class BayesUCB(ThompsonSampling):
def __init__(self, bandits, N=1, gamma=3):
self.bandits = bandits
self.N = N
self.gamma = gamma
self.reset()
def select(self):
num_bandits = len(self.bandits)
bayes = [0] * num_bandits
for i in range(num_bandits):
bayes[i] = self._mean[i] + beta.std(self._alpha[i], self._beta[i]) * self.gamma
max_bandits = np.where(bayes == np.max(bayes))[0]
bandit = np.random.choice(max_bandits)
return bandit
Resultados
Ahora se puede comprobar ambos métodos con el método UCB1 para ver los resultados. Algo que se puede hacer usando la clase Bandit, definido en la entrada de Epsilon-Greedy, usando el siguiente código.
np.random.seed(0) bandits = [Bandit(0.02), Bandit(0.06), Bandit(0.10)] thompson = ThompsonSampling(bandits) ucb_n = BayesUCB(bandits) ucb_1 = UCB1(bandits) thompson.run(200000) ucb_n.run(200000) ucb_1.run(200000) thompson.plot(True, label='Thompson Sampling') ucb_n.plot(True, label='Bayes-UCB') ucb_1.plot(True, True, label='UCB1') plt.legend()
Obteniendo la siguiente gráfica.
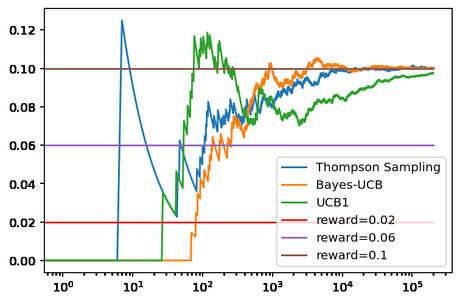
En ambos casos se puede ver que tanto el Muestreo de Thompson como BayesUCB converge antes al bandido óptimo. Lo que se pueden ver en el número de veces que ha jugado cada uno de ellos con los bandidos que no son óptimos. En el caso del Muestreo de Thompson se ha seleccionado un bandido no óptimo 406 veces (117 + 289), para BayesUCB han sido 593 veces (68 + 525) y para UCB1 son 11.339 (2680+ 8719) las veces que se ha seleccionará uno de los bandidos no óptimos. Lo que nos indica que usar la distribución Beta para estos bandidos es una buena solución.
Quizás el mayor problema que tiene tanto el Muestreo de Thompson como BayesUCB es que necesitan mucho más tiempo que otros para seleccionar al mejor bandido. Esto es así por la necesidad de evaluar la función beta en ambos casos.
Conclusiones
En esta ocasión hemos visto dos métodos para resolver un problema tipo bandido multibrazo: el Muestreo de Thompson y BayesUCB. Ambos métodos probabilísticos basados en ideas bayesianas. Estos métodos han demostrado seleccionar una mayor cantidad de veces el bandido óptimo al trabajar con bandidos basados en la distribución Binomial.
