La desigualdad matemática: Introducción a las inecuaciones (Clase magistral)

Estimados señores lectores: A lo largo de los años, son muchos los que me han rogado de vez en cuando colgar aquí para mis lectores algunas de mis “famosas” lecciones matemáticas que llevo años recopilando y comentando para cientos y cientos de estudiantes que han tenido el honor de haber pasado por las puertas de mi aula. Aunque es obvio que no todos vosotros sois matemáticos y seguramente tampoco os interesa estudiar matemáticas, creo que ya va siendo hora de hacer un buen repaso de algunas cosas que veo y me irritan en los libros de textos actuales. Para hacer esta primera lección lo más “accesible” posible para principiantes, es necesario tener un contexto. Por eso, voy a comparar mi lección haciendo comparaciones puntuales con el libro de texto de matemáticas que es actualmente el utilizado por la mayoría de estudiantes en España. Se trata del libro de texto de la editorial SANTILLANA, de la Serie resuelve, para 1º de Bachillerato. Utilizo esta edición específica por si quereis comprobar mis referencias bibliográficas.

Esta clase magistral me vino a la mente porque en el hilo anterior, algunas personas trataron el tema de la igualdad y un comentarista dijo que “no se puede igualar lo que no es igual”. El filósofo alemán Nietzsche le daría la razón, ya que llegó a decir “nunca iguales lo que no es igual”. Pero, ¿es cierto siempre y sobre todo, para las matemáticas? Veremos hoy muchos conceptos.

Antes que nada, os diré que los libros de texto en matemáticas de hoy en día en gran parte de Occidente son un auténtico desastre vergonzoso y nada riguroso. De hecho, en este sentido España incluso sale mejor parada que EEUU, ya que al menos el libro de la edición Santillana tiene ejercicios bastante más rigurosos si comparamos con ub libro de text estándar de matemáticas en EEUU. La razón de ello se debe a múltiples problemas políticos que no voy a tratar aquí porque es irrelevante a la lección en sí. Hay que mencionarlo, no obstante, porque si estudias matemáticas en el clima actual, verás que la lección que te daré aquí te va a dejar un poco alucinado por cosas que muy probablemente, tu libro de texto OMITE o incluso, ni siquiera tu profesor lo sabe. En el caso de España, la ventaja es que (según tengo entendido actualmente sigue así) un profesor de matemáticas debe ser MATEMÁTICO. NO es el caso en EEUU. Aquí hay profesores de matemáticas que en realidad lo que tienen es una licenciatura en “educación matemática”, PERO NO ES LO MISMO a ser matemático, como le tengo que recordar una y otra vez a mis alumnos universitarios cuando pisan mi aula y me preguntan horrorizados cosas tipo, ¿¿pero cómo que un exponente no es una potencia??” PUES NO ES UNA POTENCIA, ES UN EXPONENTE (o si se prefiere, ÍNDICE). MUCHO CUIDADO JOVEN…y ahi es donde me doy cuenta de las barbaridades que algunos profesores de secundaria enseñan. Aquí existen incluso dispositivos mnemotécnicos como el famoso PEMDAS, que me escandaliza. “PEMDAS” significa “PARENTHESIS, EXPONENTS, MULTIPLICATION, DIVISION, ADDITION, SUBTRACTION”. Lo utilizan para enseñarle a los alumnos la orden de operaciones (lo que yo llamo la JERARQUÍA de operaciones) y cuando ven que su querido pemdas no funciona en mis ejercicios de jerarquia de operaciones, alucinan en colores y me dicen “me siento estafado por mi colegio de secundaria”. Pues sí chaval, te estafaron pero bien, gracias a políticos incompetentes. En fin, no doy más la chapa con esto porque sé que siempre hay gentuza que me acusa de “politizarlo todo”.

Bien. Antes de entrar en las comparaciones con Santillana, es necesario que os de un buen repaso de lo que son las desigualdades matemáticas. Mucha atención a mi texto porque le seguirán ejercicios obligatorios si queréis que escriba la segunda parte de la entrada.

—————————
La mayoría de los que se acuerden algo de matemáticas, recordarán expresiones que son iguales. Normalmente, las igualdades se escriben como ecuaciones lineales o no lineales, pero tienen el símbolo de la igualdad. Así pues, 2 + 7= 9. 2 mas 7 es IGUAL a 9, solo que escrito de otra manera. Hoy vamos a tratar cosas que no son iguales. Si sabemos que una expresión es mayor a otra, escribimos la inecuación de esta manera: 2 + 7 > 5. El símbolo > nos dice que 2 + 7 es mayor a 5. También podriamos escribir esta relación con el 5 en la izquierda: 5 < 2 + 7. En palabras, esta inecuación nos dice que 5 es inferior a la suma de dos mas siete. Estas inecuaciones son conocidas (si eres culto en las matemáticas) como “inecuaciones estrictas” ya que un lado debe ser necesariamente mayor o inferior al otro lado. También podemos hablar de inecuaciones NO estrictas, en las que un lado es IGUAL O MAYOR al otro o MENOR O IGUAL al otro. Por ejemplo, 5 – 3 ≥ 2. El símbolo es “igual o mayor que”. De esta explicación, os comentaré/contestaré 8 preguntas (que contienen varias partes) y entonces os dejaré los ejercicios. 1. Luis es más alto que Jaume. Jaume es más alto que Viçent. ¿Es Luis más alto que Viçent? Sí, por supuesto. Ya que Luis es más alto que Jaume, se da por sentado que Luis es más alto que cualquiera que sea incluso más bajito que Jaume. Ya que Viçent es una de esas personas, sabemos que Luis es más alto que él también. Si a > b y b > c, ¿es a > c? Recordad que cuando el símbolo apunta a la derecha, significa “mayor a”, por razón de la recta real numérica.

Aquí se razona exáctamente como en el primer apartado de esta pregunta inicial. A es máyor a B y B es mayor a C. Se da por hecho entonces que A tiene que ser también mayor a C. Esto lo podemos ver en la siguiente recta numérica:

A es mayor que B (por eso está a la derecha de B) y lo mismo pasa con la b respecto a la c. B es mayor a C, por eso B está a la derecha. Podemos juntar todo esto y formar lo que se llama una “cadena de desigualdades”: a > b > c.

Si a > b y b < c, podemos saber si a o c es mayor? Si a > b y c > b, ¡entonces no sabemos cómo relacionarnos con la a o la c! Por ejemplo, podríamos tener a = 3, b = 2, y c = 4, mirad lo que tendriamos: (3 > 2, 4 > 2), lo cual nos daría c > a (4 > 3). Ó, también podriamos tener el caso de a = 4, b = 2, y c = 3.

(4 > 2, 3 > 2), lo cual nos daría c < a (3 < 4)!! MUY IMPORTANTE: Si a > b y b > c, entonces a > c. Con la misma lógica, si a ≥ b y b ≥ c, a ≥ c.

Bien. Pasemos a la Segunda pregunta. ¿Qué pasa? ¿Creeis que ya está y listo? No, no, no, aquí nos tomamos muy en serio los temas como para despachar las cosas con rapidez y superficialidad.
————————-
2. Bill Gates tiene más dinero que Warren Buffett. Si los dos ganan un premio de 100 millones de dólares, ¿Bill Gates seguirá teniendo más dinero que Buffett? ¿Y si los dos aportan 100 millones de dólares a nuestro proyecto de Liberalismo Democrático? ¿Cual de los dos tendrá más dinero?

Si los dos ganan un premio de 100 millones de dólares, los dos van a tener el mismo aumento sobre el dinero del que YA disponian. Siendo así, la diferencia seguirá entre los dos. Es decir, Gates seguirá teniendo más dinero que Buffett.

Con la misma lógica, si los dos nos dan a nosotros 100 millones de dólares (una idea estupenda, porque nosotros creemos en cierta redistribución de la riqueza) seguirán siendo diferentes. Gates seguirá siendo más rico que Buffett (pero eso sí, podriamos hacer cosas impresionantes desde Liberalismo Democrático con ese dinero…incluido la completa destrucción de medios libertarianos y anarcocapitalistas).

¿Cuál de las dos es mayor — 7 + 2 o 5 + 2? ¿7 – 9 o 5 – 9? Para cualquier número “a”, ¿cuál es mayor, 7 + a o 5 + a?

Dejemos que x > y, a > b y c > 0. Expliquemos por qué x + c > y + c.

Ya qye x > y, sabemos que la x debe estar a la derecha de y en la recta real. Cuando sumamos c a cada una, nos movemos en pasos c a la derecha. En otras palabras, x + c y y + c están a c pasos a la derecha de x e y, respectivamente. Así como demuestra mi gráfica siguiente:

Explica por qué x – c > y – c.

Restar es ir a la izquierda en la recta numérica. Funciona igual que sumar, solo que vas en sentido izquierda. Así:

Explica por qué x + a > y + b.

Si podemos sumar ecuaciones, también podemos sumar inecuaciones. Si x > y a > b, (a y b son positivos). Siendo así, sabemos que x está a la derecha de y y sumarle a lo mueve más a la derecha. Es decir, como x es mayor a y, está más adelantado en la recta si se compara con y. X ya empezaba con ventaja respecto a y, por eso x + a está más a la derecha que y + b. Matemáticamente, pues,

x + a > y + b.

Así pasa en la vida también: hay quienes nacen con ventajas que otros no tienen y se acercan más así a la prosperidad. No existe la igualdad de oportunidades realmente.

También hubiesemos podido razonar esto sin recurrir a la recta numérica. Sabemos que x > y, asi que x + a > y + a. Sabemos que a > b, asi que si sumamos y a los dos lados nos da y + a > y + b. En consecuencia, x + a > y + a > y + b.

Nótese que 7 > 5 y 3 > 2 y que 7 + 2 > 5 + 3. ¿Es siempre verdadero que si x > y y a > b, entonces x + b > y + a?

¡PUES NO! Nótese que 9 > 8 y 5 > 2, pero 9 + 2 NO ES > 8 + 5. Si lo único que sabemos es que x > y o a > b, no podemos saber cual es mayor, si x + b o y + a. ¡A lo mejor hasta son iguales!

Como podeis ver, Nietzsche era interesante, pero desde luego a pesar de su amor por las matemáticas (bueno, admiración más bien, parece que se saltó el capítulo de inecuaciones…o quizá no y le daba igual).

IMPORTANTE:

Si x > y, entonces x + c > y + c para cualquier número real c. Si también tenemos a > b, entonces x + a > y + b.

Bueno, ya hemos abordado la suma y la resta de inecuaciones a nivel más básico (porque en la segunda entrada hay mucho más que comentar).

Ahora entremos en la multiplicación y división.

————————————
3. Si x > y, ¿es verdad entonces que xa > ya?

Debemos demostrar algo sobre los productos. Lo único que sabemos sobre productos e inecuaciones es que el producto de dos números positivos siempre es mayor a 0. Veremos si podemos utilizar ese concepto.

Ya tenemos un número positivo: a. Como x > y, podemos restar y o sumar (-y) a los dos lados de la inecuación para obtener:

x – y > 0. Dáte cuenta que x – y es otro número POSITIVO. El producto de los números positivos a y (x – y) es positivo, así que tenemos:

(x – y)a > 0. Ampliando el lado izquierdo utilizando las leyes de distribución, tenemos: xa – ya > 0. Sumando ya a los dos lados:

xa – ya + ya > 0 + ya ——- xa > ya.

¡Por fin! Ahora podemos tener la prueba para nuestras leyes de productos y cocientes de las inecuaciones:

Si x > y siendo también a > 0, entonces xa > ya. Si x ≥ y (a mayor que 0), entonces xa ≥ ya.

4. Supongamos que x, y, a y b son todos números positivos, y que x > y y a > b. ¿Es verdad entonces que xa > yb?
¿Es verdad que x/a > y/b? ¿Y si nos permiten que nuestras incógnitas sean negativas?

A nivel intuitivo, parece claro que xa > yb, ya que multiplicamos dos números “grandes” y dos números “pequeños”. Podemos utilizar el resultado del problema anterior para ver que xa > ya y ya > yb. Colocando xa > ya y ya > yb juntos nos da:

xa > ya > yb. Siendo así, xa > yb.

Si dejamos que CUALQUIERA de estas incógnitas sea negativa, entonces no podemos decir nada en general sobre xa y yb, porque cualquiera de los dos productos puede ser negativos.

Tampoco podemos concluir que x/a > y/b. Por ejemplo, supongamos que x=4, y=1, a=7 y b=1. Siendo así, x > y, a > b. Pero entonces, x/a es mayor a y/b.

IMPORTANTE:

Si x > y > 0 y a > b > 0, entonces xa > yb. Si x ≥ y > 0 y a ≥ b > 0, entonces xa ≥ yb.

Bien, ya con esto liquidamos la multiplicación y la división de números positivos. Hemos visto que debemos tener mucho cuidado cuando tratamos con números negativos (al igual que cuando tratamos con personas negativas y antisociales que ponen en peligro el ordenamiento del estado social).

¿Qué podemos decir sobre la multiplicación y división de números negativos?

5. Si x > y con a < 0, ¿qué podemos sobre las cantidades xa y ya?

Podemos intentar algunos ejemplos. 7 x (-4) = -28 y 5 x (-4) = -20. Siendo así, 7 x (-4) < 5 x (-4). ¡Anda! ¿Qué ha pasado? Al parecer, cuando multiplicamos una inecuación válida por un número negativo, ¡tenemos que REVERTIR el símbolo! Podemos pensar que si x > y y a < 0, entonces xa < ya. A ver si podemos explicar por qué esto es cierto. A estas alturas, todos debéis saber (y si no lo sabes, no deberías estar ingresado en la universidad sino en primaria), que el producto de un número positivo multiplicado por un número negativo es NEGATIVO. Por el hecho de que x > y, tenemos x – y > 0. Así que a es negativa y x – y es positivo. Entonces el producto (x-y)a es negativo, lo cual significa:

(x-y)a < 0
xa – ya < 0
xa < ya Bien, ya sabemos multiplicar o dividir una inecuación por un número negativo.

6. Si a es un número positivo, ¿qué es mayor? 7 elevado al a o 5 elevado al a? Ya hemos visto que si x > y > 0 y que a > b > 0, entonces xa > yb. Aquí, tenemos 7 > 5 > 0 asi que 7 x 7 > 5 x 5. Por esa razón,

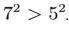
Si a es un número positivo que no sea 1, ¿qué cantidad es mayor de las siguientes?

ó

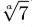
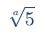
Bueno, esto parece mucho a lo anterior. Aquí tenemos que usar las leyes de las potencias.

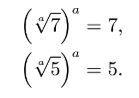
7. Luego está el hecho de que si x es un número real, entonces x elevado al cuadrado siempre será igual a 0 o mayor. Esto se llama una inecuación “trivial”. Como muchas ideas sencillas, también es muy poderosa. La exploraremos con más detalle en otro momento.

8. Supongamos que x e y son números positivos tales que x > y. ¿Qué cantidad es mayor? ¿1/x o 1/y? ¿Y si y es negativo y x es positivo?

Experimentemos.

Sabemos que 7 > 5 y que 1/7 4/3 y que 2/5 -1/2 y 1/5 > -2, así que claramente no siempre revertimos la inecuación cuando tomamos la inversa de los dos lados. La diferencia en este ejemplo es que un lado es positivo, otro negativo.

Hemos demostrado, pues, que si tomamos la inversa de los dos lados de una inecuación, REVERTIMOS el símbolo si los dos lados son POSITIVOS.

¿Qué os ha parecido mi clase magistral? Dejad vuestros comentarios (positivos o negativos)…pero creo que he sido riguroso y absolutamente más detallado que cualquier libro de texto de esta época.

Os dejo con 5 ejercicios.
———————————————-
1. Si x ≤ y y x ≥ y, entonces ¿qué vale x – y?

2. Si a ≥ b y b > c, entonces ¿es cierto que a > c? ¿Es posible que a = c?

3. Suponed que x > y > 0 y que a > b > 0. ¿Es cierto que x/b > y/a? Si es así, ¿por qué? Si no es así, aporta un ejemplo en el que
x/b ≤ y/a y x > y > 0 y a > b > 0.

4. Suponed que x < y < 0. Demuestra que 1/x es inferior a 1/y.

5. Suponed que x > y > 0 y a es un número entero NEGATIVO. ¿Qué cantidad es mayor? x elevado al indice a o y elevado al indice a?