“Ábaco de Fibonacci” en Pisa

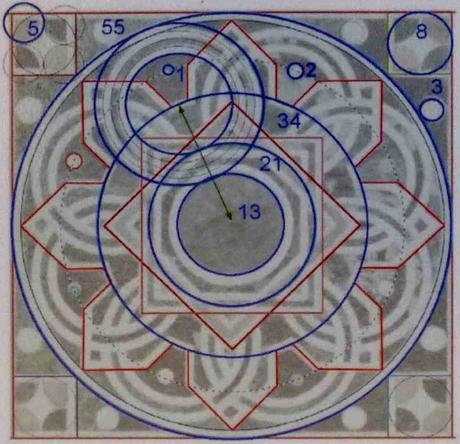
La fachada de la iglesia de San Nicola muestra un curioso trabajo de taracea geométrica en mármol que llamó la atención del profesor Pietro Armenti (1957 – 2019), quien enseñaba en la cercana Facultad de Geología. Armenti comprobó que la relación entre el diámetro del círculo menor y el mayor era 55, el undécimo término de la sucesión de Fibonacci: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…Continuando las relaciones entre círculos van saliendo el resto de los términos de la sucesión, tal como se muestra en el diagrama del cartel explicativo del “descubrimiento”.

Leonardo Pisano (c. 1170 – c. 1240), conocido como Fibonacci, fue un matemático destacado en la incorporación del saber arábigo al mundo cristiano a través desde su inicial Liber abaci (1202). La dinámica República de Pisa mantenía relaciones comerciales en el Mediterráneo y el padre de Leonardo parece que le llevó a Bugía (hoy en Argelia) donde aprendió la numeración indo-arábiga y la aritmética práctica.

La sucesión de Fibonacci es de tipo recurrente, cada término es suma de los dos anteriores (a _n = a _n-1 + a _n-2) y es la solución del problema de la reproducción de los conejos que Pisano enunció.

Reproducimos el cartel donde el municipio detalla y referencia los trabajos del profesor Armenti. Solemos ser algo escépticos ante estas “coincidencias” pero el estudio de ellas nos parece muy atractivo en este caso. Como la “divina proporción” (o “número áureo”) es el límite del cociente de dos términos consecutivos de la sucesión de Fibonacci, quizá puede haberse buscado conscientemente la belleza de las proporciones.