Cuando aprendemos sobre reticulados nos enseñan un algoritmo para conseguir la matriz de la relación de predecesores inmediatos de un CPO (Conjunto Parcialmente Ordenado) [A,
] donde A tiene n elementos.El algoritmo sería el siguiente:
-Se calcula la matriz de la relación de orden M
.-Determinamos la matriz M = M
- In . M es igual a la matriz de relación de orden menos la matriz identidad.-Calculamos M^2 (M al cuadrado = MxM) haciendo una multiplicación binaria. Es decir, la matriz resultante solo contendrá unos y ceros como entradas.
-Hallamos M< = M - M^2 (matriz de la relación predecesor inmediato). La matriz de la relación predecesor inmediato es igual a la matriz M menos la matriz M^2.
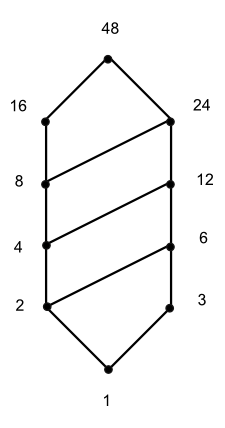
Ejercicio de ejemplo:
Dado el CPO [A, /] en donde A = {200,60,30,10,5,1} y "/" es la relación binaria de divisibilidad en A, (a/b si y sólo si "a" divide a "b") entonces: Hallar la matriz de predecesores inmediatos.
Siguiendo el algoritmo calculamos la matriz M
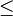:1 5 10 30 60 200 1 | 1 1 1 1 1 1 | 5 | 0 1 1 1 1 1 |M
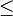= 10 | 0 0 1 1 1 1 | 30 | 0 0 0 1 1 0 | 60 | 0 0 0 0 1 0 | 200 | 0 0 0 0 0 1 |1 divide a todo número real, por ello todas las entradas de esta fila de la matriz son 1.
5 divide a 5, 10, 30,60,200.
10 divide a 10,30,60,200.
30 divide a 30 y 60.
60 divide a 60.
200 divide a 200.
Siguiente paso, calculamos la matriz M que esta dada por M = M
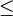- In.1 5 10 30 60 200
1 | 1 1 1 1 1 1 | - | 1 0 0 0 0 0 |
5 | 0 1 1 1 1 1 | - | 0 1 0 0 0 0 |
M
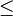= 10 | 0 0 1 1 1 1 | - In = | 0 0 1 0 0 0 |30 | 0 0 0 1 1 0 | - | 0 0 0 1 0 0 |
60 | 0 0 0 0 1 0 | - | 0 0 0 0 1 0 |-
200 | 0 0 0 0 0 1 | - | 0 0 0 0 0 1 |
| 0 1 1 1 1 1 |
| 0 0 1 1 1 1 |
M = | 0 0 0 1 1 1 |
| 0 0 0 0 1 0 |
| 0 0 0 0 0 0 |
| 0 0 0 0 0 0 |
Luego, calculamos M^2:
| 0 1 1 1 1 1 | | 0 1 1 1 1 1 |
| 0 0 1 1 1 1 | | 0 0 1 1 1 1 |
M = | 0 0 0 1 1 1 | x M = | 0 0 0 1 1 1 |
| 0 0 0 0 1 0 | | 0 0 0 0 1 0 |
| 0 0 0 0 0 0 | | 0 0 0 0 0 0 |
| 0 0 0 0 0 0 | | 0 0 0 0 0 0 |
| 0 0 1 1 1 1 |
| 0 0 0 1 1 1 |
M^2 = | 0 0 0 0 1 0 |
| 0 0 0 0 0 0 |
| 0 0 0 0 0 0 |
| 0 0 0 0 0 0 |
Finalmente, hallamos la matriz de la relación predecesor inmediato.
| 0 1 0 0 0 0 |
| 0 0 1 0 0 0 |
M< = | 0 0 0 1 0 1 |
| 0 0 0 0 1 0 |
| 0 0 0 0 0 0 |
| 0 0 0 0 0 0 |
C++
Una buena opción es desarrollar este algoritmo en algún lenguaje de programación que conozcamos, con el fin de aprender un poco más y a su vez comprobar los ejercicios que realizamos en nuestras horas de estudio. Este algoritmo lo podemos desarrollar en c++ de la siguiente forma:
#include <iostream>
using namespace std;
int main(){
int filas, colum;
cout << "Ingrese la cantidad de filas de la matriz de la relación de orden: " << endl;
cin >> filas;
cout << "Ingrese la cantidad de columnas de la matriz de la relación de orden: " << endl;
cin >> colum;
int matrizRO[filas][colum]; //matriz de relación de orden
int matrizRO2[filas][colum];
int matrizm2[filas][colum];
int matrizPI[filas][colum];
// Ingresamos las entradas de la matriz de relación de orden
cout << "Ingrese las entradas de la matriz de la relación de orden" << endl;
for(int i = 0; i < filas; i++){
for(int j = 0; j < colum; j++){
cout << "Ingrese la entrada a" << i << j << endl;
cin >> matrizRO[i][j];
}
}
// Restamos la matriz identidad a nuestra matriz
for(int diagonal = 0; diagonal < colum; diagonal++)
{
matrizRO[diagonal][diagonal] = 0;
}
//Imprimimos el valor de M
cout << "Matriz M: " << endl;
for(int i = 0; i < filas; i++){
for(int j = 0; j < colum; j++){
cout << matrizRO[i][j] << " ";
}
cout << endl;
}
//segunda matriz
for(int i = 0; i < filas; i++){
for(int j = 0; j < colum; j++){
matrizRO2[i][j] = matrizRO[i][j];
}
}
//
//Calculamos M^2 (Binarizada)
for(int i=0;i<filas;i++){
for(int j=0;j<colum;j++){
matrizm2[i][j]=0;
for(int k=0;k<colum;k++){
if(matrizRO[i][k] == 1 and matrizRO2[k][j] == 1)
matrizm2[i][j] = 1;
}
}
}
// Imprimimos M^2
cout << "Matriz M^2: " << endl;
for(int i = 0; i < filas; i++){
for(int j = 0; j < colum; j++){
cout << matrizm2[i][j] << " ";
}
cout << endl;
}
//Calculamos la matriz de la relación predecesor inmediato
for(int i = 0; i < filas; i++){
for(int j = 0; j < colum; j++){
matrizPI[i][j] = matrizRO[i][j] - matrizm2[i][j];
}
}
//Imprimimos la matriz de la relación predecesor inmediato
cout << "Matriz de la relación predecesor inmediato: " << endl;
for(int i = 0; i < filas; i++){
for(int j = 0; j < colum; j++){
cout << matrizPI[i][j] << " ";
}
cout << endl;
}
return 0;
}
int matrizRO[filas][colum]; //matriz de relación de orden
int matrizRO2[filas][colum];
int matrizm2[filas][colum];
int matrizPI[filas][colum];
La matrizRO representa la matriz de relación de orden, la matrizRO2 contiene las mismas entradas que la anterior, esta se usará solo para realizar la multiplicación para obtener M^2.La matrizm2 representa la matriz M^2.La matrizPI representa la matriz de la relación de predecesores inmediatos.
int filas, colum;
cout << "Ingrese la cantidad de filas de la matriz de la relación de orden: " << endl;
cin >> filas;
cout << "Ingrese la cantidad de columnas de la matriz de la relación de orden: " << endl;
cin >> colum;
Inicialmente ingresamos la cantidad de filas y columnas que tiene nuestra matriz. Dicha matriz es una matriz cuadrada de orden nxn.
//Restamos la matriz identidad a nuestra matriz
for(int diagonal = 0; diagonal < colum; diagonal++)
{
matrizRO[diagonal][diagonal] = 0;
}
Para encontrar el valor de M solo debemos anular la diagonal principal de nuestra matriz.
//Calculamos M^2 (Binarizada)
for(int i=0;i<filas;i++){
for(int j=0;j<colum;j++){
matrizm2[i][j]=0;
for(int k=0;k<colum;k++){
if(matrizRO[i][k] == 1 and matrizRO2[k][j] == 1)
matrizm2[i][j] = 1;
}
}
}
Calculamos M^2 con el anterior algoritmo, tomar en cuenta que como es una matriz binarizada solo tendrá ceros y unos. Al conseguir una coincidencia de dos 1 almacenamos 1 en la matriz M^2.
//Calculamos la matriz de la relación predecesor inmediato
for(int i = 0; i < filas; i++){
for(int j = 0; j < colum; j++){matrizPI[i][j] = matrizRO[i][j] - matrizm2[i][j];
}
}
Calculamos la matriz de la relación de predecesor inmediato con la diferencia entre la matriz M y M^2.
Resolviendo el ejercicio anterior con nuestro programa de consola hecho en c++, ésta sería su ejecución:
Ingrese la cantidad de filas de la matriz de la relación de orden:
6
Ingrese la cantidad de columnas de la matriz de la relación de orden:
6
Ingrese las entradas de la matriz de la relación de orden
Ingrese la entrada a00
1
Ingrese la entrada a01
1
Ingrese la entrada a02
1
Ingrese la entrada a03
1
Ingrese la entrada a04
1
Ingrese la entrada a05
1
Ingrese la entrada a10
0
Ingrese la entrada a11
1
Ingrese la entrada a12
1
Ingrese la entrada a13
1
Ingrese la entrada a14
1
Ingrese la entrada a15
1
Ingrese la entrada a20
0
Ingrese la entrada a21
0
Ingrese la entrada a22
1
Ingrese la entrada a23
1
Ingrese la entrada a24
1
Ingrese la entrada a25
1
Ingrese la entrada a30
0
Ingrese la entrada a31
0
Ingrese la entrada a32
0
Ingrese la entrada a33
1
Ingrese la entrada a34
1
Ingrese la entrada a35
0
Ingrese la entrada a40
0
Ingrese la entrada a41
0
Ingrese la entrada a42
0
Ingrese la entrada a43
0
Ingrese la entrada a44
1
Ingrese la entrada a45
0
Ingrese la entrada a50
0
Ingrese la entrada a51
0
Ingrese la entrada a52
0
Ingrese la entrada a53
0
Ingrese la entrada a54
0
Ingrese la entrada a55
1
Matriz M:
0 1 1 1 1 1
0 0 1 1 1 1
0 0 0 1 1 1
0 0 0 0 1 0
0 0 0 0 0 0
0 0 0 0 0 0
Matriz M^2:
0 0 1 1 1 1
0 0 0 1 1 1
0 0 0 0 1 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
Matriz de la relación predecesor inmediato:
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 1
0 0 0 0 1 0
0 0 0 0 0 0
0 0 0 0 0 0
Optimizando el algoritmo en c++:
El código fuente del algoritmo hecho en c++ está escrito con el mayor detalle posible con el fin de que pueda ser entendido fácilmente. Sin embargo, este puede ser optimizado evitando la creación de algunas matrices no tan necesarias y algunos ciclos repetitivos for. Esto con el fin de minimizar el tiempo de ejecución y reducir el espacio utilizado en la memoria.
#include <iostream>
using namespace std;
int main(){
int n;
char respuesta;
do{
cout << "Ingrese el valor de n para su matriz de orden nxn " << endl;
cin >> n;
int matrizR[n][n]; //matriz de relación de orden y luego de la relación predecesor inmediato.
int matrizm2[n][n];
// Ingresamos las entradas de la matriz de relación de orden
cout << "Ingrese las entradas de la matriz de la relación de orden" << endl;
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
cout << "Ingrese la entrada a" << i << j << endl;
cin >> matrizR[i][j];
//Anulando diagonal principal al momento de ingresar la matriz
if(i == j)
matrizR[i][j] = 0;
}
}
//Calculamos M^2 (Binarizada)
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
matrizm2[i][j]=0;
for(int k=0;k<n;k++){
if(matrizR[i][k] == 1 and matrizR[k][j] == 1)
matrizm2[i][j] = 1;
}
}
}
//Calculamos la matriz de la relación predecesor inmediato y la imprimimos al mismo tiempo
cout << "Matriz de la relación predecesor inmediato:" << endl;
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
matrizR[i][j] = matrizR[i][j] - matrizm2[i][j];
cout << matrizR[i][j] << " ";
}
cout << endl;
}
cout << "Desea obtener una nueva matriz de la relación predecesor inmediato a partir de otra matriz de relación de orden? si = s no = n" << endl;
cin >> respuesta;
}while(respuesta == 's');
return 0;
}
Inicialmente ingresamos el valor de n, la matriz de la relación de orden es una matriz cuadrada de orden nxn.
Mientras ingresamos las entradas o componentes de la matriz podemos ir anulando automática la diagonal principal, esto lo hacemos cuando los índices i y j son iguales.
if(i == j)
matrizR[i][j] = 0;
Al momento de obtener la matriz de la relación predecesor inmediato podemos guardar el resultado en la misma matriz inicial, además podemos ir imprimiendo los resultados en paralelo se van obteniendo.
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
matrizR[i][j] = matrizR[i][j] - matrizm2[i][j];
cout << matrizR[i][j] << " ";
}
cout << endl;
}
Descarga del código fuente del proyecto:
http://www.mediafire.com/download/urr...
También te podría interesar:
4 Ejercicios Básicos de Programación Orientada a Objetos en c++
De sistema decimal a sistema binario en c++ y Java
3 libros sobre programacion orientada a objetos
[Ejercicio resuelto c++ POO Herencia Vectores MVC] Una Asociación de Lancheros trasladan turistas
Puzzle Bobble
Karate Blazers
Puzzle De Bloques
Magical Cat Adventure