Al hacer figuras de Origami, es imposible no notar los ángulos que se forman al plegar. Por eso quiero hablar de este tema, que creo es muy importante.
Pues bien, pongamos de ejemplo un ¨cuadrado¨.

Si lo plegamos en una de sus diagonales, vamos a obtener un ¨triángulo¨.

Si tratamos de plegar ese ¨triángulo¨ como ¨oreja de conejo¨, podremos observar que se forman estos ¨ángulos¨.

Al doblar un ¨cuadrado¨ por su diagonal obtenemos un ¨triángulo¨, el cual, tiene un ángulo de 90° y 2 de 45°. Al querer hacer una ¨oreja de conejo¨ tenemos que plegar un ángulo de 45° a su mitad, esto es para que el lado del ¨triángulo¨ quede encima de su ¨base¨. Pues bien, el ángulo que obtenemos de esto es el de 22.5°.
Hacia el otro extremo, si es que no hemos terminado la técnica de ¨oreja de conejo¨, podemos observar como es que se forma otro ¨triángulo de 45°-90°-45°¨.
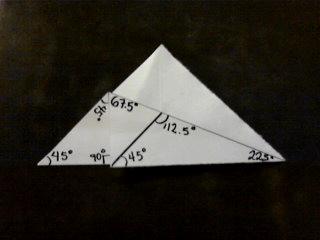
Si ahora analizamos como esta formada la ¨base Cometa¨, podemos darnos cuenta de que son los mismos ángulos que mencionaba anteriormente.

Si hacemos la ¨base de pez¨, es lo mismo.


Noten que el ángulo de 135° es el mismo al que me refiero en el ¨procedimiento reloj de arena¨.

Ahora, analicemos la ¨base de pájaro¨. Comencemos haciendo la ¨base preliminar¨. Vemos que se forman puros triángulos de 45°-90°-45°.



Pues si, así es, al hacer la ¨base de pájaro¨ estuvimos haciendo los mismos pliegues, por lo tanto, obtenemos los mismos ángulos.
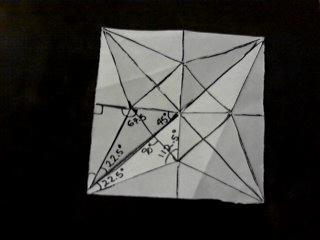
Ahora es el turno de la ¨base de rana¨.




Por lo que podemos observar, encontramos los mismos ángulos que vimos en las figuras anteriores, aunque están en una posición diferente.
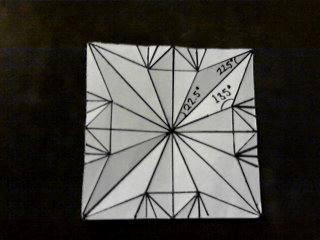
Aquí expongo, las 3 bases, la de ¨pez¨, la de ¨rana¨ y la de ¨pájaro¨, con sus respectivos ángulos.

Podemos llegar a la conclusión de que se utilizan los mismos ángulos en estas bases. Pero, ¿por qué?... pues porque en todas utilizamos el ¨triángulo¨ de 45°-90°-45°. Aunque se obtienen resultados muy diferentes con cada base, el ¨núcleo¨ de cada una de ellas es la utilización del mismo tipo de ¨triángulo¨.
Entonces, ¿qué podemos hacer para cambiar los ángulos?... Pues cambiar los ¨triángulos¨.
¿Qué tal si ahora utilizamos un ¨triángulo¨ de 60°?
Para hacer este triángulo, ¨origamísticamente¨ hablando, debemos observar el lado superior y el de la derecha del cuadrado de la siguiente foto. Se dividide en 4 partes cada lado, entoces debemos unir la punta inferior izquierda con 1/4 de la parte de arriba y con 1/4 de la derecha. Cada quien puede escoger los puntos a utilizar, aquí sólo muestro un ejemplo.
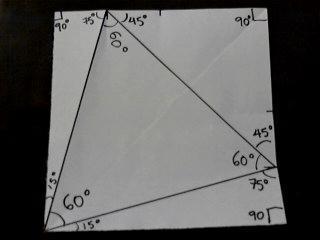
Si dividimos a la mitad el triángulo de 60° obtendremos el triángulo de 30°-90°-60°. Como dato extra, esto me trae recuerdos de la ¨escuela Secundaria¨, en la que llevaba como clase ¨Dibujo técnico Industrial¨. Aquí, las herramientas básicas que utilizabamos eran las ¨escuadras¨ de 45° y la de 30°-60°.

Si volvemos al tema de los ángulos, nos damos cuenta que el triángulo de 60° esta formado por 4 triángulos iguales de 60°. Al ver los dobleces marcados y los 4 triángulos no puedo evitar recordar a la ¨trifuerza¨ que aparece en ¨La leyenda de Zelda¨, uno de mis videojuegos favoritos, jejeje.
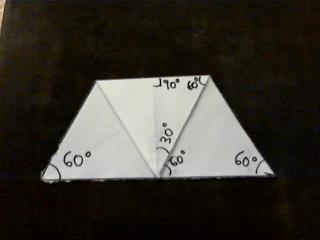
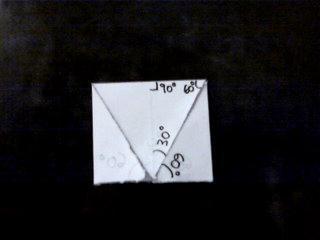


Aquí me pregunté, ¿cómo se vería una ¨oreja de conejo¨ en uno de estos triángulos?

Pues se forma un triángulo de 30°-120°-30°.

Ahora, ¨juguemos¨ un poco con el triángulo de 45°.
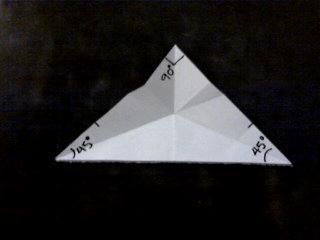




Por último, hagamos una ¨base de pájaro¨ con los 2 triángulos centrales, o sea, con el rombo, un ¨cuadrado deformado¨. Y en los triángulos restantes de sus ¨extensiones¨, en uno una ¨oreja de conejo¨ y en el otro una ¨doble oreja¨ y ¨estirando¨ su punta central.
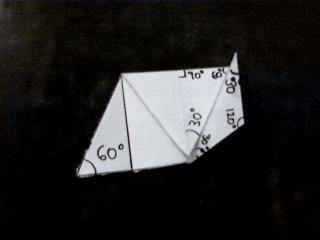

Para mayor facilidad, primero hacer la ¨base de pájaro¨.




¿Qué podremos hacer con una ¨base de pájaro¨ alargada y con esas ¨extensiones¨?
Etiquetas: Origami, Papiroflexia
