Aplicaciones y un poquito de historia de las cónicas.

1.- Algo de historia.

• Menaechmus (siglo IV a.C.): mostró que las cónicas se obtienen al cortar un cono por planos no paralelos a la base
• Apollonio de Perga (siglo III a.C.): el primero que las introdujo públicamente, escribiendo “Las Cónicas”, el más importante tratado antiguo sobre las secciones cónicas.

Motivo: buscar soluciones sólo con regla y compás de los tres famosos problemas griegos. ¿Cuáles eran? Trabajo para cuando tengáis tiempo!!! 

• Galileo (siglo XVI): demostró que las trayectorias de los proyectiles son

parabólicas.

• Kepler (siglo XVII): rescató las cónicas al encontrar en la elipse la respuesta al enigma del movimiento planetario, descubriendo que el planeta Marte tiene órbitas elípticas y el sol está situado en uno de sus focos.

• Newton (siglo XVII): enunció la famosa ley de la gravitación universal, en base a este descubrimiento; así el descubrimiento de Kepler se deduce como consecuencia matemática de dicha ley.

2.- Propiedades de las cónicas
Apolonio demostró que las cónicas tienen muchas propiedades interesantes. De entre todas ellas destacan, las llamadas propiedades de reflexión. Si se construyen espejos con la forma de una curva cónica que gira alrededor de su eje, se obtienen los llamados espejos elípticos, parabólicos o hiperbólicos, según la curva que gira. Apolonio demostró que si se coloca una fuente de luz en el foco de un espejo elíptico, entonces la luz reflejada en el espejo se concentra en el otro foco. Si se recibe luz de una fuente lejana con un espejo parabólico de manera que los rayos incidentes son paralelos al eje del espejo, entonces la luz reflejada por el espejo se concentra en el foco. Esta propiedad permite encender un papel si se coloca en el foco de un espejo parabólico y el eje del espejo se apunta hacia el sol. Existe la leyenda de que Arquímedes (287-212 A.C.) logró incendiar las naves romanas durante la defensa de Siracusa usando las propiedades de los espejos parabólicos. En el siglo XVI el filósofo y matemático René Descartes (1596-1650) desarrolló un método para relacionar las curvas con ecuaciones. Este método es la llamada Geometría Analítica. En la Geometría Analítica las curvas cónicas se pueden representar por ecuaciones de segundo grado en las variablesxey. El resultado más sorprendente de la Geometría Analítica es que todas las ecuaciones de segundo grado en dos variables representan secciones cónicas se lo debemos a Jan de Witt (1629-1672).En la actualidad las cónicas aparecen en nuestras vidas casi sin darnos cuenta:

• La propiedad de reflexión de la parábola se usa para los telescopios y las antenas de televisión. La propiedad análoga, que nos dice que un rayo que parte del foco se refleja paralelamente al eje sirve para que los faros de los automóviles concentren el haz en la dirección de la carretera o para estufas. Así mismo, Las trayectorias de los proyectiles tienen forma parabólica. Los chorros de agua que salen de un surtidor tienen también forma parabólica

• Las órbitas de los planetas alrededor del sol son elípticas (el sol se encuentra en uno de los focos). La excentricidad de la órbita de la Tierra alrededor del Sol es aproximadamente 0,0167. La de mayor excentricidad es la órbita de Plutón, 0,2481, que incluso es pequeña. Los cometas y los satélites también describen órbitas elípticas (algunos incluso pueden tener órbitas elípticas e hiperbólicas). En el extremo contrario está el cometa HALLEY cuya excentricidad es de 0,9675, muy próxima a 1. Así mismo, en medicina se usa la litotripsia (revolucionaria técnica para el tratamiento de problemas en el riñón). Usa ondas sonoras intensas generadas fuera del cuerpo del paciente para pulverizar las piedras y convertirlas en arena que pueda ser fácilmente eliminada por el organismo. La clave está en enfocar las ondas para que sólo al cálculo. Para ello se usa una cámara semielipsoidal. En uno de sus focos se crea una poderosa chispa que evapora agua. La parte que golpea el reflector converge en el otro foco, donde se encuentra la piedra, con toda su intensidad, provocando su destrucción.

• El sistema LORAN (long range navigation), sistema de navegación por radio. Permite determinar la posición a partir de la diferencia de recepción de las señales de radio procedentes de dos emisores sincronizados distantes entre sí.

3.- ¿Por cuántos puntos pasa como mínimo?

• Dados 2 puntos cualesquiera, existe una única recta que pasa por ellos.
• Dados tres puntos cualesquiera no alineados, existe una única circunferencia que contiene a estos tres puntos (esta circunferencia estarácircunscritaal triángulo definido por estos puntos) Su ecuación es:

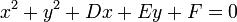
• Dados 5 puntos con tres no alineados, existe una única cónica que contiene a estos cinco puntos. La ecuación de una cónica cualquiera viene dada por: