Area Under the Curve: Feedback and Explanation

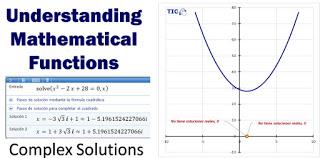
Área bajo la curva: Retroalimentación y explicación.

Para calcular el área bajo la curva es indispensable determinar si existen partes de dicha área que se encuentran debajo del eje equis, ya que en tal caso se obtendría un área negativa introduciendo un error en la integral o cualquier otro método que se utilice para dicho cálculo. Este tema fue abordado en una explicación previa que se encuentra en el enlace siguiente:
http://licmata-math.blogspot.com/2020/03/area-under-curve-part-2.html
Procedimiento de solución problema 1 del ejercicio 2.1. Área bajo la curva.
1. Leer el ejercicio e interpretarlo:
            Determina el área bajo la curva: y = x^2 - 2x + 1 + NL entre: x1 = 0 y x2 = 3
            Considerando que el número de lista del alumno es 27 la ecuación queda:
                                                             y = x^2 - 2x + 28
2. Determinar si, dentro del intervalo indicado (x1 = 0, x2 = 3) exite una solución de la ecuación.
Vamos a buscar las raíces de la ecuación, ya que en caso de que dicha raíz esté entre 1 y 3       tendríamos que considerar áreas positivas y negativas. Ppodemos utilizar cualquier calculadora o software para resolver la ecuación.
Empleando la hoja de cálculo que se proporcionó nos encontramos con que la ecuación no tiene soluciones reales.

Si utilizamos cualquier otra herramiemta tecnológica como calculadoras o programas de cómputo nos arroja un resultado en números complejos:
                              x1 = 1 - 5.1962i
                              x2 = 1 + 5.1962i
Sin importar la herramienta empleada el significado es el mismo, la curva no corta al eje equis en ningún punto, para estar seguros trazamos la gráfica con cualquier herramienta; aplicaciones de celular, programas de cómputo, o sencillamente tabulamos unos pocos puntos, o puede usarse el archivo que se proporciónó anteriormente y se encuentra en:
http://licmata-math.blogspot.com/2020/03/use-of-technology-in-education-01.html
En este caso, y dado que de ahora en adelante contaremos con esta herramienta vamos a utilizar el programa que resuelve y grafica ecuaciones de segundo grado y obtenemos la gráfica:
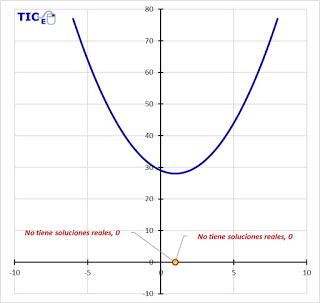Tal como lo comentamos anteriormente, la curva no toca al eje equis, por lo tanto, el área se calculará directamente, sin necesidad de considerar áreas de signo negativo.
3. Determinar el área por el método indicado en el problema.

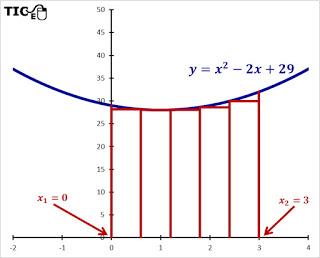
Aplicando la integral con una calculadora ciencífica se obtiene:

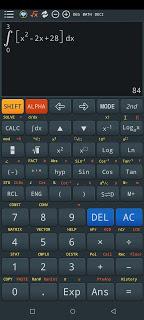
4. Obtener las áreas por el método de rectángulos empleando Excel para facilitar la operatividad.
Esperamos que sea de utilidad.
Saludos.