ARITMETICA: Proporcionalidad

Problema
[Nivel:Intermedio]
La grafica muestra los valores correspondientes de dos magnitudes A y B, donde en el tramo \( \overline{OM} \)son Directamente Proporcionales pero en tramo \( MN \) la relación es Inversamente Proporcional.


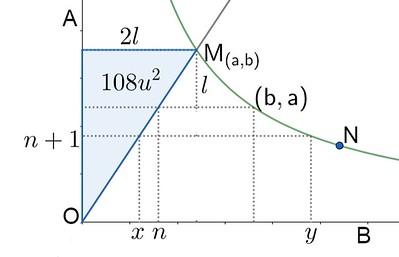
Calcular \( "x+y" \)
Solución
Completando el gráfico con los datos dados:

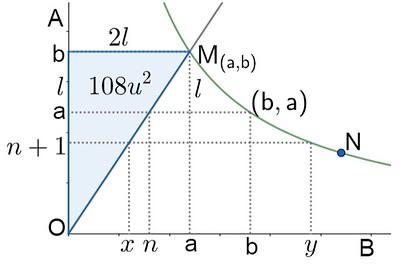
Del gráfico tenemos:
\( a = 2l \quad ... (i) \\ b - a = l \quad ... (ii) \\ \rightarrow \quad b = 3l \quad ... (iii) \)
Del área del triángulo:
\( 108 = \cfrac{(2l)(b)}{2} \\ \rightarrow \quad lb=108 \quad ... (iv) \)
De \( (iii) \) en \( (iv) \)
\( lb=108 \\ \rightarrow \quad l(3l) = 108 \\ \rightarrow \quad l = 6 \)
Reemplazando en \( (i) \) y \( (iii) \):
\( a = 12 \\ b = 18 \)
Dado que en el tramo \( \overline{OM} \) la relación es Directamente Proporcionales, entonces:
\( \cfrac{b}{a} = \cfrac{a}{n} = \cfrac{n+1}{x} \)
Reemplazando los valores de a y b:
\( \underbrace{\cfrac{18}{12} = \cfrac{12}{n}}_{(*)} = \cfrac{n+1}{x}\quad ... (iv) \)
De \( (*) \) tenemos que \( n = 8 \)
Reemplazando \( n \) en \( (iv) \) se tiene que \( x = 6 \)
En el tramo \( MN \) la relación es Inversamente Proporcionales, por tanto:
\( ab=y(n+1) \)
Reemplazando los valores de \( a,b,n\) tenemos que \( y=24 \)
Luego tenemos que \( x+y \) es 30.
ARITMETICA Problema 20