
Uno de los conflictos más reiterados en las empresas industriales es la no siempre comprendida tensión entre los departamentos de comercial y producción.
Por experiencia profesional reconozco que esta tensión inter-departamental no es una leyenda urbana o un lugar común sino un hecho real que obedece a causas profundas, sistémicas, que van más allá del desgaste personal o emocional de sus responsables o la existencia de buenos canales de información.
Con el ánimo de contribuir a resolver este conflicto de raíz, me permito enunciar algunas reflexiones en forma de axiomas y corolarios para aportar un grano de arena en orden a disipar este conflicto, ubicando su solución en la encrucijada estratégica entre el significado profundo de optimizar y el rol decisivo de la dirección general. Vamos allá.
Axioma 1: Una planificación óptima de la producción es aquella que mejor representa los objetivos de la Dirección General de la empresa en un momento histórico dado.
Axioma 2: Se entiende que los objetivos emanados de la Dirección General de la empresa se corresponden con preferencias estratégicas y que estas son transitivas, es decir, que existe una relación de orden o priorización entre ellas (a > b > c...), es decir, satisfacen el teorema de imposibilidad de Arrow (no es posible diseñar un sistema que permita reflejar las preferencias locales en una preferencia global), pues dado que en todo sistema de producción con recursos finitos e interdependientes es habitual la existencia de conflictos entre preferencias/objetivos ( p.ej. el "eterno" conflicto entre los departamentos comercial y producción), no existe una solución que optimice de forma simultánea todas las funciones objetivo, dejando aparte las llamadas "soluciones de compromiso", que no son óptimas en modo alguno o los llamados "óptimos de Pareto" que mediante "aproximaciones sucesivas" tienden a igualar la importancia o prioridad de las preferencias.
Corolario 1: No existe ningún sistema de optimización con preferencias transitivas que pueda satisfacer todas las preferencias/objetivos por igual. Se hace necesaria una subordinación y supraordinación entre preferencias/objetivos.
Axioma 3: Las reglas de programación estándar APS ( Advanced Planning and Scheduling) tienden a priorizar una función objetivo o preferencia: Minimizar tiempos de preparación, Minimizar retrasos, minimizar WIP ( Work in Process), Secuencia preferida por recurso, Campañas, Programación de Cuellos de Botella, Saturación de líneas, etc. atendiendo además a las restricciones de los recursos del sistema (calendarios, turnos, disponibilidad de sub-recursos, disponibilidad de materiales, etc.).
Axioma 4: Además de las reglas estándar APS, herramientas como Preactor-SIEMENS permiten crear reglas compuestas para aplicar selectivamente las reglas estándar, además de crear reglas personalizadas con las que poder satisfacer nuevas preferencias/objetivos.
Corolario 2: No existe una regla de programación que satisfaga por igual todas las preferencias/objetivos. Todo decisor debe elegir. Toda elección implica renunciar y toda renuncia implica un coste de oportunidad: conocer ese coste nos da la clave de la mejor preferencia/objetivo: la que mayor utilidad nos ofrezca ( parábola de los cañones o la mantequilla de Paul Samuelson). No obstante, en ausencia de "objetivos fuertes" cabe la posibilidad de considerar el coste como objetivo o preferencia a minimizar, atendiendo al "principio de la palanca": p.ej. es más interesante mover un cuerpo pesado haciendo palanca que con el sobreesfuerzo voluntarioso de muchos recursos. Los dos métodos son igual de eficaces ( se obtienen resultados), pero el primero es más eficiente ( se obtienen resultados minimizando los recursos).
Consecuentemente: se debe establecer un sistema de ordenación de las preferencias/objetivos (SOP), que no obstante puede variar en el tiempo por circunstancias del mercado, política de la compañía, segmentación de producto/mercado, etc. por tanto se entiende que el SOP puede ser configurable.
Una vez establecidas las preferencias/objetivos, se trata de que la Dirección General ordene de mayor a menor el conjunto de las mismas: p.ej. Minimizar costes de preparación (por agrupación de productos o formato) > Minimizar costes en un periodo determinado (por lanzamiento de campañas) > Maximizar la ocupación de recursos (programación "push" o Just in Case) > Minimizar WIP (valor del stock en curso) > Minimizar retrasos (programación "pull" o Just in Time) > Minimizar sobrecostes por retrasos (evitar penalizaciones de clientes mediante priorizaciones) > Maximizar margen de contribución por producto (por priorización de productos con mayor valor añadido)... (Ver Observación).
Corolario 3: Dados los Axiomas 3 y 4, cada regla de programación tenderá a maximizar un "indicador clave de rendimiento" o KPI ( Key Performance Indicator).
Axioma 5: Para establecer un sistema de optimización basado en reglas con preferencias/objetivos excluyentes, se necesita una regla de reglas, es decir, una regla de alto nivel o metarregla que establezca la mejor regla de programación de acuerdo al criterio de ordenación que se establezca, considerando la propiedad de que toda metarregla tenderá a optimizar unas preferencias/objetivos mientras suboptimiza otras ( p.ej. si quiero optimizar el consumo de combustible de mi vehículo deberá suboptimizar mis prisas por llegar).
Corolario 4: Existen dos posibles métodos de establecimiento de metarreglas:
Corolario 4.1: Método Iteractivo o en cascada: por cada regla de programación se comparan los KPI's, de mayor a menor orden de preferencia/objetivo, seleccionado la regla que mayor KPI obtenga en la primera preferencia y en caso de empate de KPI con otra/s regla/s se selecciona de entre ellas la regla que mayor KPI obtenga en la segunda preferencia y así sucesivamente.
Corolario 4.2: Método Sintético: se establece un KPI de síntesis o "indicador sintético" que represente el valor compuesto de todos los KPI's de cada regla para obtener un indicador sintético por cada regla, seleccionando la regla con el indicador sintético mayor. Hay varios métodos para calcular un indicador sintético, siendo la más sencilla la aplicación de una ponderación o peso a cada KPI, una ponderación en coherencia con la ordenación de preferencias/objetivos.
Observación: se puede observar que existen preferencias contradictorias entre sí, sin embargo estas pueden ordenarse de manera distinta según el periodo del año: p.ej. hacia el principio de la campaña puede ser más importante minimizar el coste por cambio de formato (mejorar los costes) que minimizar los retrasos (empeorando el servicio) al fabricar "tiradas más largas" contra stock o previsión, mientras que hacia mediados/finales de campaña puede ser más importante lo contrario, esto es, minimizar retrasos (mejorar el servicio) que minimizar el coste del cambio de formato (empeorando el coste) al fabricar "tiradas más cortas" o contra pedido. Estas contradicciones se pueden representar como un dilema coste vs. servicio en el siguiente gráfico.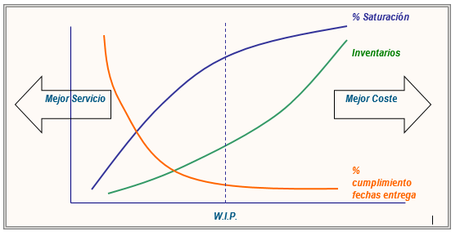
- Equilibrar el flujo, no la capacidad.
Es decir, ajustar el flujo por el cuello de botella con la demanda del mercado. Si como hemos visto, la cadencia del Sistema está marcada por los cuellos de botella, hagamos que estos (y con ellos todo el Sistema) coincidan con el flujo de la demanda. De manera que cuando necesitemos aumentar la capacidad de la Empresa para acercarla a la demanda, esto signifique explotar sólo los cuellos de botella. En muchas ocasiones las empresas intentan aumentar la capacidad de tal o cual recurso esperando con ello ser más "competitivo", cuando en realidad (si estamos de acuerdo con las implicaciones de la TOC) no es precisamente la mejor alternativa desde el enfoque sistémico. La mayor eficiencia de la empresa en su conjunto nos vendrá de una mayor fluidez y sincronización entre los recursos.
- El grado de utilización de un no cuello de botella no vendrá determinado por su propia capacidad, sino por alguna otra restricción del sistema.
Es decir, no intentemos aumentar la "productividad" de los recursos que no sean cuellos de botella. Produciremos Inventario y Gastos de Operación, pero no Facturación. Antes al contrario, que su "productividad" esté sincronizada con los recursos cuello de botella. O lo que es lo mismo, que los recursos no cuello de botella no produzcan más rápido de lo que pueden absorber los cuellos de botella. Esto tiene implicaciones importantes en los modelos de productividad clásica. En muchas empresas industriales se adquiere stock simplemente para que máquinas y empleados no estén "parados". Evidentemente así quien controla el flujo de materiales y de trabajos no son los pedidos o los programas de producción sino la Inercia.
- Activar un recurso no es lo mismo que utilizar ese recurso.
Ya que, "utilizar" un recurso significa hacer uso de él para que el Sistema se dirija hacia la Meta. En la regla anterior, si hacemos un uso no sincronizado de un recurso no cuello de botella, no estamos utilizando ese recurso, sino simplemente activándolo en términos locales, es decir sin dirección hacia el objetivo último del Sistema. En un momento determinado en cualquier empresa pueden estar activados una gran cantidad de recursos: personas, locales, comunicaciones, energía, ordenadores, máquinas, etc. pero... ¿Cuáles realmente de esos recursos se están utilizando en orden a la Meta de la empresa?.
- No se debe intentar optimizar cada uno de los recursos del Sistema. Un Sistema con óptimos locales no es un Sistema óptimo en su conjunto. De hecho es un Sistema muy ineficiente.
Es la conclusión de las dos reglas anteriores. Ya lo hemos visto antes, dado que existen esos dos fenómenos, a saber, Fluctuaciones Estadísticas y Recursos Dependientes, cualquier intento de optimizar un recurso por sí mismo, de acuerdo exclusivamente a su capacidad, es como mínimo una falta de perspectiva. Desgraciadamente la Productividad se ha entendido como un parámetro excesivamente localista, lo que nos ha llevado a enormes stocks de materiales, obras en curso máximas, grandes cantidades de producto acabado y... rentabilidades mínimas.
- Una hora perdida en un cuello de botella significa una hora perdida para todo el Sistema.
Los sistemas contables tradicionales asignan los costes de los recursos en función de parámetros tales como amortización, energía, salarios, etc. es decir, otra vez el enfoque analítico, no sistémico de lo que ocurre en la Empresa. Si tal como hemos visto, los recursos cuello de botella determinan en última instancia el ritmo de todo el Sistema, cualquier parada o reducción de la capacidad de los mismos no nos "cuesta" sólo lo que contablemente podamos imputarle a ese recurso aisladamente, sino mucho más. ¿Cuánto?, pues tanto como cuesta el Sistema en su conjunto durante esa parada.
- Una hora ganada en un no cuello de botella es un espejismo.
Esta es la otra cara de la moneda. Lo que es cierto para los recursos cuello de botella no lo es para los que no lo son. Es un error perder tiempo en un recurso cuello de botella, sin embargo, perderlo en los recursos no cuello de botella es posible, incluso conveniente para el Sistema en su conjunto. ¿Por qué?, porque "ahorrar" tiempo en los no cuellos de botella no aumenta el rendimiento del Sistema para nada. El tiempo y el dinero ahorrado ahí son una ilusión. En otras palabras, si intentamos "ocupar todo el tiempo" de los recursos que no sean cuello de botella produciremos más Inventario y más Gastos de Operación, pero no más Facturación.
Fuente jmonzo.blogspot.com/2015/02/axiomas-para-una-planificacion-optima.html

