Catálogo de componentes de redes neuronales (II): funciones de activación

En el artículo anterior de este blog, hablamos sobre los tipos de capas más habituales que se utilizan en redes neuronales, empezando así un breve trabajo de catalogado de las opciones de diseño de que se dispone en redes neuronales, pensando muy especialmente en Deep Learning.

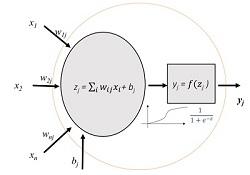
Neurona artificial. Fuente: Jordi Torres

En este segundo artículo de esta breve serie, vamos a hablar de las funciones de activación. Como se recoge en la figura (autoría de Jordi Torres) y que ya utilizamos en el artículo anterior, una neurona artificial habitualmente divide su procesamiento en dos partes. Por un lado un tratamiento de las entradas (que puede ser, por ejemplo, una suma ponderada como se muestra en la figura o una convolución) y, al resultado de esa primera función, aplicarle otra pequeña transformación para obtener el valor de salida de nuestra neurona. Esa segunda transformación, esa segunda función que en la figura se representa dentro de un rectángulo, es a lo que se denomina función de activación y es un segundo elemento de diseño relevante.
Existe una cierta variedad de funciones de activación, algunas de las cuales se muestran en la figura.

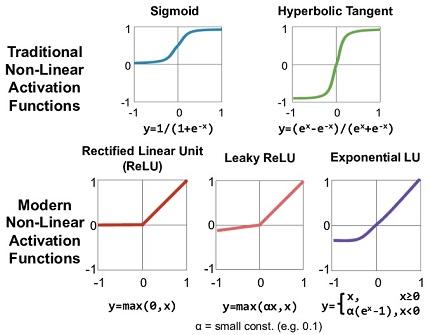
No vamos a verlas todas, pero sí mencionar algunas de las más habituales.

• Función Lineal: Se trata, quizá, del caso más simple, en que la función de activación básicamente, da una salida igual a la entrada, es decir, actúa como función identidad trasladando a su salida el resultado obtenido en la primera parte del procesamiento de la neurona (la suma ponderada de entradas, por ejemplo).


• Función Rectified Linear Unit ('ReLU'): Aunque el nombre pueda llamar a engaño, se trata en realidad de una función no lineal. En este caso, el valor de la función de activación es igual a su entrada mientras ésta sea mayor que cero (en ese caso sí actúa como lineal) pero, en caso contrario, el valor de activación es nulo. Su labor, en el fondo, no es más que eliminar valores negativos. Es difícil de explicar brevemente, pero este tipo de no linealidades aumenta las posibilidades de la red. En concreto, esta función, muy popular, da buenos resultados, por ejemplo, en redes de convolución y, por tanto, en tareas como visión artificial o reconocimiento de voz. Aparte de la ReLU, existen otras muchas funciones de activación que juegan con la linealidad y no linealidad de forma parecida, como pueden ser, por ejemplo, la 'Leaky ReLU' en que para los valores negativos se proporciona una pendiente diferente (más tendida) que para los positivos o la 'Exponential LU'.


• Función Sigmoidea (logística): Se trata de una función continua y derivable (importante en los algoritmos de aprendizaje), con un rango entre 0 y 1 y generalmente cerca de esos extremos (0 ó 1). Esto la hace muy adecuada para problemas de clasificación. Por ejemplo, para una clasificación binaria, una única neurona de salida con esta función de activación sigmoidea tendería a dar muy bien el resultado (cercano a uno una categoría, cercana a cero la otra). También se utiliza en problemas de regresión con salida entre 0 y 1.


• Función Tangente Hiperbólica: Una función con una forma parecida a la sigmoidea pero que, en este caso, proporciona valores entre 1 y -1, es decir, admite valores negativos en la salida.


• Función 'softmax' (función exponencial normalizada): Es una función de activación un poco particular, puesto que la salida no sólo depende de las entradas de la neurona sino también de la salida de las otras neuronas de la misma capa. Cuando se aplica una función de activación, la suma de las activaciones de la capa debe ser 1. Se utiliza en problemas de clasificación en múltiples categorías y etiquetas, en las que cada neurona de salida representa una categoría. La que tiene el valor más alto es la que representa con más probabilidad la categoría que corresponde a los datos mostrados en la entrada de la red.

Existen más funciones de activación, claro, pero con éstas mencionadas creo que se cubren los casos más habituales, así que podemos cerrar por ahora el catalogado. En el siguiente paso iremos a por los algoritmos de aprendizaje.
Artículos de este blog relacionados

• Catálogo de componentes de redes neuronales (I): capas
• Estructura de una red neuronal y el inicio de una catalogación sencilla