Catálogo de componentes de redes neuronales (III): funciones de pérdida

Continuando con el catálogo de elementos de diseño, en este post vamos a hacer un catalogado básico de las funciones de pérdida ('loss functions').
¿Qué es una función de pérdida?
La función de pérdida, también denominada función objetivo, en esencia, nos dice, durante el proceso de entrenamiento de la red, lo lejos que está en un momento dado, lo que la red nos ofrece como salida y el resultado que nosotros consideramos que es el correcto o deseado. El valor de la función de pérdida será luego un dato de entrada en el algoritmo de aprendizaje.
Dado que los algoritmos de aprendizaje como el descenso de gradiente, calculan la derivada de la función de pérdida, ésta debe ser una función continua y derivable. 
Hay una gran variedad de funciones de pérdida posibles pero para nuestro catálogo sencillo, y basándonos en los libros 'Deep Learning con Python' de François Choillet y 'Python Deep Learning' de Jordi Torres, seleccionamos las siguientes:

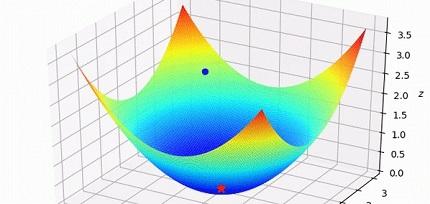
• Error Cuadrático Medio ('Mean Square Error', MSE): Una función muy conocida que calcula la distancia 'geométrica' al valor objetivo. Hablar de distancia geométrica es una forma de visualizarlo que nos orienta cuando pensamos en dos o tres dimensiones. Más allá de esas dimensiones, es sólo una forma de entenderlo. Además, decimos distancia, pero en realidad es la distancia elevada al cuadrado. Una variante de ésta seria la que, en lugar del cuadrado de la distancia, elige el valor absoluto ('Absolute Error'). MSE se puede usar, por ejemplo, en problemas de regresión a valores arbitrarios y con una última capa sin función de activación.


• Entropía cruzada Categórica ('Categorical Cross Entropy'): Sin entrar en detalles, la entropía cruzada, en general, es una medida de la distancia entre distribuciones de probabilidad. La entropía cruzada suele ser adecuada en modelos de redes cuya salida representa una probabilidad, como cuando hacemos una clasificación categórica con función de activación 'softmax'. Se puede utilizar, por ejemplo, en problemas de clasificación categórica con una sola etiqueta de salida y precedida de una función de activación 'Softmax'.


• Entropía cruzada binaria ('Binary Cross Entropy'):  Una variante de la anterior pero en que tratamos con clasificación binaria y , por tanto, la función de activación sería una sigmoide.


• Entropía Cruzada Categórica Dispersa ('Sparse Categorical Cross Entropy'): Una variante que se suele usar en el caso de trabajar con números enteros.

Hay mucho más aparato matemático detrás de las funciones de pérdida, y más opciones posibles pero, en aras de la simplicidad que busco, también en mi propio provecho, dejaremos nuestro catálogo limitado estas cuatro y sin entrar en la formulación matemática exacta de las funciones.
En el próximo artículo de este catálogo ya atacaremos al aprendizaje propiamente dicho. 
Artículos de este blog relacionados

• Catálogo de componentes de redes neuronales (II): funciones de activación
• Catálogo de componentes de redes neuronales (I): capas
• Estructura de una red neuronal y el inicio de una catalogación sencilla