
Nuestra numeración indoarábiga es una notación posicional, lo que significa que la posición de cada dígito contribuye a su valor, siendo así más sencillo sumar unidades con unidades, decenas con decenas, centenas con centenas, etc. Sin embargo, en los sistemas numerales como el romano, algunos números pueden representarse con un dígito mientras cifras intermedias ocupan más posiciones. ¿Cómo lograban realizar cálculos con este sistema?
La respuesta es que no tenían profesores de primaria que les dijeran "No uses la calculadora" y simplemente recurrían al ábaco. Estos ábacos tenían varias columnas para cada una de las potencias de 10 (I, X, C, M...). En cada una se colocaban unas cuentas o guijarros llamadas cálculos ( calculi) o bronces ( acra) que representaban la cantidad de lo que estuvieran contando. Estas columnas podían estar divididas en dos. En la mitad inferior, las cuentas seguían representando el valor de una unidad en esa columna, mientras las cuentas en de la mitad superior se correspondían con cinco unidades de la mitad inferior de esa columna o la mitad del valor de las cuentas de la siguiente.
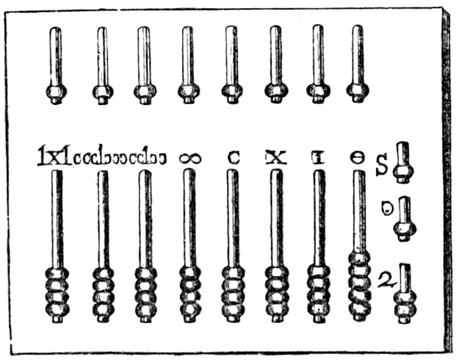
La suma y la resta se hacía de la misma manera que actualmente, representando representaba el primer número con las cuentas, añadiendo o quitando cuentas en cada columna y llevándonoslas a la columna contigua cuando se superan el número de cuentas en la anterior. Cuando las columnas del ábaco estaban divididas en dos mitades, esto ocurría cuando la mitad superior contenía al menos dos cuentas. A su vez, la mitad superior se rellenaba cuando la inferior alcanzaba cinco cuentas.
La multiplicación era más complicada y no todos la ejecutaban. Primero se representaban ambos números a multiplicar en el ábaco. Tened en cuenta que en una mesa que extienda las filas, con varios ábacos o la suficiente memoria y práctica, se pueden representar ambos números sin que se mezclen la cuentas. Como se hace actualmente, cada columna de un número se multiplica con las columnas del otro, sumando los productos resultantes de estas operaciones. Sobre la división, se han propuesto métodos, pero se desconoce cómo la hacían los romanos y los griegos, de quienes aprendieron.
Por último, quizás te habrás preguntado para qué son las columnas de la derecha del ábaco. Eran ranuras relativas al as, la moneda. La segunda ranura, con una O, tenía una parte superior con una sola cuenta y una inferior con cinco. Estas representaban las uncia, la doceaba parte del as, por lo que al superar seis cuentas en la mitad inferior, se añadía una a la superior. Cuando lo hacía de nuevo, se hacía en la ranura del as.
El uso de ábacos y mesas de cálculo sobrevivió al imperio romano en Europa, pero los números arábigos y los cálculos en papel fueron tomando terreno en la Edad Media. Como algunos cálculos requerían de buenas dotes para manejar el ábaco y una formación especializada, temían por la competencia, los abaquistas frenaron el avance de los algoristas. Como ocurrió con la adopción del cero, este avance fue desigual, siendo adoptada primero por matemáticos y astrónomos, mientras en las finanzas y el comercio se mantuvo el ábaco hasta la Revolución Francesa.
- Ifrah, G. (2000). The universal history of numbers: From prehistory to the invention of the computer. Wiley.
- Schlimm, D., & Neth, H. (2008). Modeling ancient and modern arithmetic practices: Addition and multiplication with Arabic and Roman numerals. In CogSci (pp. 2097-2102).

