El Museo de Arte Medieval de las Termas de Cluny en el barrio latino de París presenta como su principal atractivo la admirable serie de tapices de la Dama del Unicornio. Del delicioso tapiz de la Aritmética ya hemos hablado, corresponde ahora fijarse en un modesto dado de marfil de 14 caras (un tetrakaidecaedro).
Los cinco sólidos platónicos convexos son ideales para hacer dados por su perfecta simetría. Los poliedros regulares de 4, 6, 8, 12 y 20 caras serían fáciles de realizar y son conocidos desde la Grecia Clásica. Los icosaedros ya se usaron como dados en Alejandría.
Los sólidos arquimedianos no son nada adecuados para hacer dados por la gran diferencia de tamaño de sus caras pero el ingenio puede suplir las deficiencias. El Museo Cluny nos muestra un dado que utiliza el octaedro truncado, sólido de Kelvin, como referencia para su construcción.
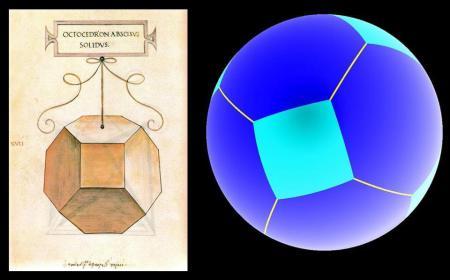
Si se fabricara un dado con el octaedro truncado sería inservible: sus ocho caras hexagonales tendrían más del doble y medio de superficie que sus seis cuadrados. Si se hace la esfera ortogonal del poliedro la diferencia de superficie es similar. El dado favorecería ocho caras en detrimento de las otras seis.
La solución adoptada en el dado del Cluny es mantener la esfera y ahuecar en forma de casquete esférico invertido los centros de las caras de la proyección ortográfica. La solución no es perfecta pues las zonas de influencia siguen siendo muy diferentes pero ya no es abismal dinámicamente, sobre todo si se agrandan los seis casquetes de las caras cuadradas. Nos gustaría haber medido y probado el dado pero hemos de conformarnos con dejar constancia.
El dado se localiza en una bonita mesa repleta de juegos.
Puzzle Bobble
Karate Blazers
Puzzle De Bloques
Magical Cat Adventure