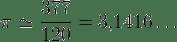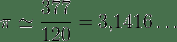π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:
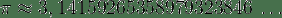
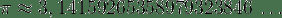
El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e. Cabe destacar que el cociente entre la longitud de cualquier circunferencia y la de su diámetro no es constante en geometrías no euclídeas.
El matemático griego Arquímedes ( siglo III a. C.) fue capaz de determinar el valor de π entre el intervalo comprendido por 3 10/71, como valor mínimo, y 3 1/7, como valor máximo. Con esta aproximación de Arquímedes se obtiene un valor con un error que oscila entre 0,024% y 0,040% sobre el valor real. El método usado por Arquímedes era muy simple y consistía en circunscribir e inscribir polígonos regulares de n-lados en circunferencias y calcular el perímetro de dichos polígonos. Arquímedes empezó con hexágonos circunscritos e inscritos, y fue doblando el número de lados hasta llegar a polígonos de 96 lados.
Alrededor del año 20 d. C., el arquitecto e ingeniero romano Vitruvio calcula π como el valor fraccionario 25/8 midiendo la distancia recorrida en una revolución por una rueda de diámetro conocido.
En el siglo II, Claudio Ptolomeo proporciona un valor fraccionario por aproximaciones:
Puzzle Bobble
Karate Blazers
Puzzle De Bloques
Magical Cat Adventure