El problema del chocolate infinito (y su solución)

Como he visto que el problema de las tres hijas que puse el otro día le ha molado al personal, hoy comparto con vosotros este pequeño fragmento de sabiduría matemática que tiene el sugerente nombre del problema del chocolate infinito. En este caso una imagen vale más que mil palabras, y la cosa es como sigue:

Posiblemente algunos os hayáis quedado picuetos después de ver la imagen. Entonces si doblo esto, y hago esto otro... ¡tengo una onza más!
Habrá algunos malpensados que piensan que esto, con un chocolate de verdad, no puede hacerse... bien, para ellos va este vídeo:

Ahora, lo importante de estos posts que estoy haciendo no es exponer el problema, porque para eso ya hay muchas páginas webs en mil sitios, sino exponer la solución. ¿Por qué ocurre este milagro que podría acabar con el hambre en el mundo? ¿Estamos ante una versión para adictos al cacao de la multiplicación de los panes y los peces?
Aunque a veces la matemática parezca magia negra, en este caso no estamos violando las leyes de la física, en concreto la concerniente a la conservación de la materia. El truco consiste en una redistribución inteligente de la geometría de modo que todo parece ser igual.
Lo primero de todo, si quitamos una onza, eso quiere decir que en el nuevo chocolate debe faltar el área equivalente a esa onza, porque si tuviéramos un chocolate entero nuevo, seríamos el nuevo Mesías. El asunto es que ese área, que parece muy grande, puede ser escondida si la dotamos de una nueva forma, del mismo modo que un piso de 5 metros de ancho y 6 de largo tiene los mismos metros cuadrados que uno de 1 metro de ancho y 30 de largo, pero yo no pagaría para vivir en el segundo.
El área de esa onza ha sido estirada a lo largo de toda una fila de onzas del chocolate final. De ese modo una fila, en realidad, es un poquito más pequeña aunque no lo parece:

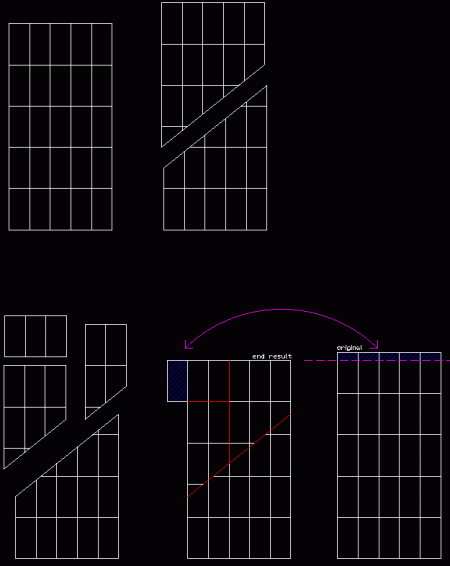
En esta página web engloban este truco visual en las llamadas paradojas geométricas, que hacen lo mismo siguiendo diferentes variantes. De todas ellas, mi favorita indiscutible es esta que os pongo aquí abajo y que os recomiendo que dibujéis en un papel cuadriculado:

Si sólo os quedáis mirándola sin dibujar, os garantizo que os va a estallar la cabeza, porque en apariencia, no hay nada incorrecto en los dibujos. El truco de esta paradoja me parece mucho más bonito y curioso que en el caso del chocolate infinito (aunque sea menos 'vendible' que la idea de conseguir eternamente onzas de la nada). El truco está en que los triángulos de color azul y rojo no tienen sus hipotenusas paralelas. Es decir, que la hipotenusa del triángulo grande no es una línea recta sino quebrada. No tenéis más que dibujarlo para comprobarlo.
Lo bonito de esto, sin embargo, radica en dos cosas:
a) Si hacéis el dibujo triángulo a triángulo en un papel cuadriculado, y luego lo enseñáis a un amigo, no va a ser capaz de ver el truco. Se quedará mirándolo durante minutos y minutos. Y si se lo enseñáis a alguien de ciencias como un matemático, flipará aún más, porque no es nada tonta la explicación que hay detrás.
b) La explicación se debe a una cosa que seguro muchos habéis escuchado alguna vez: los números de Fibonacci. Estos números cumplen una muy bonita propiedad, y es que el cociente de dos de ellos consecutivos tiende a parecerse cada vez más a un número clave de las matemáticas: el número áureo o de oro, también conocido como el canon de la belleza. En el caso del dibujo, el triángulo azul tiene de catetos 2 y 5, que son dos números de Fibonacci separados por uno de distancia (los números de Fibonacci empiezan 1, 1, 2, 3, 5, 8, 13, 21...). El triángulo rojo tiene de catetos los números de Fibonacci 3 y 8, de nuevo separados por un solo número (el 5). Y el triángulo grande tiene de catetos 5 y 13, de nuevo dos números de Fibonacci separados uno de distancia. Esto implica que las fracciones 5/2, 8/3 y 13/5 tienden a parecerse mucho, y dado que esas fracciones son las pendientes de los triángulos, a eso se debe que nuestra vista pueda ser engañada... incluso sabiendo dónde está el truco.
¡Espero que os haya gustado!