DESCRIPCIÓN DE LA ESCUADRA Y EL CARTABÓN

Una escuadra tiene dos lados iguales, es un triángulo rectángulo isósceles. Posee un ángulo de 90º y dos de 45º. Los catetos de la escuadra son los lados del cuadrado, y la hipotenusa es la diagonal, las proporciones entre los catetos y la hipotenusa vienen determinados por esta relación. Si tenemos que:
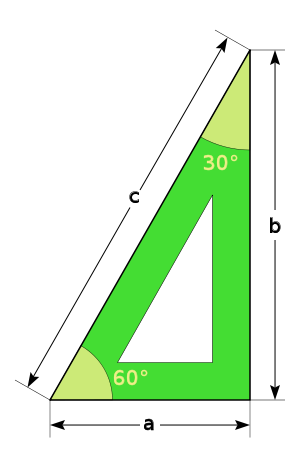 Un cartabón es una plantilla con forma de triángulo rectángulo escaleno que se utiliza en dibujo técnico. Pueden ser de diferentes tamaños y tener una escala gráfica, para usarse como instrumento de medición. Su forma es la de un triángulo cuyos ángulos son 90º, 60º y 30º. La hipotenusa mide el doble que el cateto pequeño.Sabiendo que:
Un cartabón es una plantilla con forma de triángulo rectángulo escaleno que se utiliza en dibujo técnico. Pueden ser de diferentes tamaños y tener una escala gráfica, para usarse como instrumento de medición. Su forma es la de un triángulo cuyos ángulos son 90º, 60º y 30º. La hipotenusa mide el doble que el cateto pequeño.Sabiendo que:MANEJO DE LA ESCUADRA Y EL CARTABÓN EN EL DIBUJO TÉCNICOA continuación os muestro un powerpoint con los distintos usos de estas plantillas:Escuadras
USO DE TRIÁNGULOS RECTÁNGULOS PARA REPLANTEAR EN CAMPO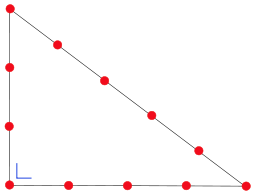 Si queremos representar un triángulo rectángulo, el más fácil es el Triángulo Egipcio o Triángulo de los 12 nudos, es el nombre moderno dado a un triángulo rectángulo cuyo lados tienen las longitudes 3, 4 y 5, o sus medidas guardan estas proporciones. Es el triángulo rectángulo más fácil de construir y, posiblemente, se utilizó para obtener ángulos rectos en las construcciones arquitectónicas desde la más remota antigüedad.
Si queremos representar un triángulo rectángulo, el más fácil es el Triángulo Egipcio o Triángulo de los 12 nudos, es el nombre moderno dado a un triángulo rectángulo cuyo lados tienen las longitudes 3, 4 y 5, o sus medidas guardan estas proporciones. Es el triángulo rectángulo más fácil de construir y, posiblemente, se utilizó para obtener ángulos rectos en las construcciones arquitectónicas desde la más remota antigüedad.
Ahora, imaginemos el siguiente supuesto:
Tenemos que marcar en una parcela (donde se quiere ejecutar un jardín) una línea de unos 10 metros perpendicular a un muro existente. ¿Qué necesitamos?,-3 estacas y un martillo para clavarlas.-1 cuerda no flexible de 12 metros de longitud.
-Lienza con azulete.¿Cómo marcamos esa línea perpendicular al muro?,Vamos paso por paso:
-Primer paso: Cogemos una estaca y apoyada contra el muro la clavamos en el punto de inicio de la línea que queremos marcar.
-Segundo paso: La segunda estaca también apoyada contra el muro la clavaremos a 4 metros de la primera. Así tendremos dibujado el primer lado del triángulo egipcio.
-Tercer paso: Solamente falta clavar la tercera estaca, su ubicación la marcará la cuerda de 12 metros que estará unida en sus extremos. Al pasar la cuerda dejándola estirada por las dos estacas ya clavadas la tercera se clavará a 3 metros de la primera estaca y a 5 metros de la segunda estaca. El lado de 3 metros es la línea perpendicular al muro.
-Cuarto paso: Solamente queda marcar con la lienza la línea obtenida.
Para esta solución se ha cogido un triángulo de lados enteros (3, 4 y 5), pero se pueden hacer triángulos más pequeños y más grandes, multiplicando o dividiendo los números anteriores (3, 4 y 5) por algún número, por ejemplo: Multiplicando por 6 daría 18, 24 y 30 (Cuerda de 72 m), dividiendo entre 3 daría 1, 1´33, 1´66 (cuerda de 4 m).
*Nota del autor: Gracias a la colaboración de mi hermano Pablo, profesor de matemáticas.
**Fuentes consultadas: http://es.wikipedia.org, http://www.slideshare.net

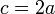
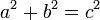




LOS COMENTARIOS (1)
publicado el 15 septiembre a las 22:33
el ale es la garrapata!!!!!!!!!! jajja