¿Qué pasa si una relación lineal no es un supuesto apropiado para nuestro modelo?
Una alternativa ampliamente propuesta por Thomas J. Sargent y John Stachurski es la estimación de máxima verosimilitud, que implica especificar una clase de distribuciones, indexadas por parámetros desconocidos, y luego usar los datos para precisar los valores de estos parámetros.
El beneficio relativo a la regresión lineal es que permite una mayor flexibilidad en las relaciones probabilísticas entre variables.
Aquí ilustramos la máxima probabilidad replicando el artículo de Daniel Treisman (2016) sobre los multimillonarios de Rusia , que conecta la cantidad de multimillonarios en un país con sus características económicas concluyendo que Rusia tiene una mayor cantidad de multimillonarios de lo que predicen factores económicos como el tamaño del mercado y la tasa impositiva.
Requeriremos las siguientes importaciones:
Configuración y suposiciones
Consideremos los pasos que debemos seguir en la estimación de máxima verosimilitud y cómo pertenecen a este estudio.
Flujo de ideas
El primer paso con la estimación de máxima verosimilitud es elegir la distribución de probabilidad que se cree que genera los datos.
Más precisamente, necesitamos suponer qué clase de distribución paramétrica está generando los datos.
- por ejemplo, la clase de todas las distribuciones normales o la clase de todas las distribuciones gamma.
Cada una de estas clases es una familia de distribuciones indexadas por un número finito de parámetros.
- Por ejemplo, la clase de distribuciones normales es una familia de distribuciones indexadas por su media. μ∈(−∞,∞) y desviación estándar σ∈(0,∞).
Dejaremos que los datos seleccionen un elemento particular de la clase definiendo los parámetros.
Las estimaciones de parámetros así producidas se denominarán estimaciones de máxima verosimilitud .
Contando multimillonarios
Treisman está interesado en estimar el número de multimillonarios en diferentes países.El número de multimillonarios se valora en números enteros.Por lo tanto, consideramos distribuciones que toman valores solo en los enteros no negativos.
(Esta es una de las razones por las que la regresión por mínimos cuadrados no es la mejor herramienta para el problema actual, ya que la variable dependiente en la regresión lineal no está restringida a valores enteros)
Una distribución entera es la distribución de Poisson , cuya función de masa de probabilidad (pmf) esf(y)=μyy!e−μ,y=0,1,2,...,∞
Podemos trazar la distribución de Poisson sobre y para diferentes valores de μ como sigue
poisson_pmf =lambda y, μ: μ**y / factorial(y) * exp(-μ) y_values = range(0, 25) fig, ax = plt.subplots(figsize=(12, 8))for μ in [1, 5, 10]: distribution = []for y_i in y_values: distribution.append(poisson_pmf(y_i, μ)) ax.plot(y_values, distribution, label=f'$\mu$={μ}', alpha=0.5, marker='o', markersize=8) ax.grid() ax.set_xlabel('$y$', fontsize=14) ax.set_ylabel('$f(y \mid \mu)$', fontsize=14) ax.axis(xmin=0, ymin=0) ax.legend(fontsize=14) plt.show()
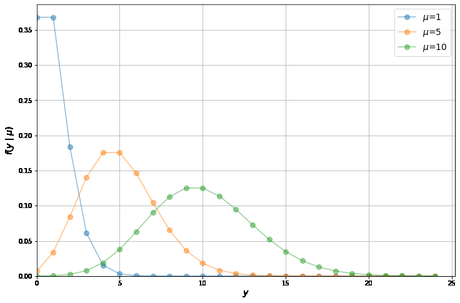
Observe que la distribución de Poisson comienza a parecerse a una distribución normal como la media de y aumenta.
Echemos un vistazo a la distribución de los datos con los que trabajaremos en esta conferencia.
La principal fuente de datos de Treisman son las clasificaciones anuales de multimillonarios de Forbes y su patrimonio neto estimado.
El conjunto de datos mle/fp.dtase puede descargar desde aquí o desde su página AER .
pd.options.display.max_columns = 10
# Load in data and view df = pd.read_stata('https://github.com/QuantEcon/lecture-python/blob/master/source/_static/lecture_specific/mle/fp.dta?raw=true') df.head()
5 filas × 36 columnas
Usando un histograma, podemos ver la distribución del número de multimillonarios por país numbil0, en 2008 (los Estados Unidos se descartan para fines de trazado)
numbil0_2008 = df[(df['year'] == 2008) & (
df['country'] != 'United States')].loc[:, 'numbil0']
plt.subplots(figsize=(12, 8))
plt.hist(numbil0_2008, bins=30)
plt.xlim(left=0)
plt.grid()
plt.xlabel('Number of billionaires in 2008')
plt.ylabel('Count')
plt.show()
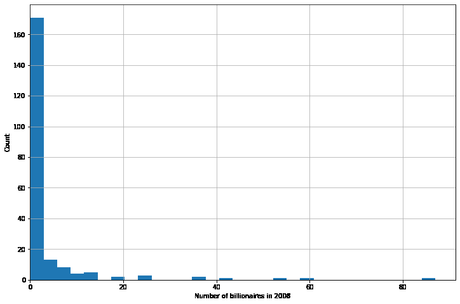
A partir del histograma, parece que la suposición de Poisson no es irrazonable (aunque con un valor muy bajo μ y algunos valores atípicos).
Distribuciones condicionales
En el artículo de Treisman, la variable dependiente: el número de multimillonarios yi en el pais i - se modela en función del PIB per cápita, el tamaño de la población y los años de pertenencia al GATT y la OMC.
Por tanto, la distribución de yi necesita estar condicionado al vector de variables explicativas xi.
La formulación estándar, el llamado modelo de regresión de Poisson , es la siguiente:(58.1)f(yi∣xi)=μiyiyi!e−μi;yi=0,1,2,...,∞.where μi=exp(xi′β)=exp(β0+β1xi1+...+βkxik)
Para ilustrar la idea de que la distribución de yi depende de xi ejecutemos una simulación simple.
Usamos nuestra poisson_pmf función de arriba y valores arbitrarios para β y xi
y_values = range(0, 20)
# Define a parameter vector with estimates β = np.array([0.26, 0.18, 0.25, -0.1, -0.22])# Create some observations X datasets = [np.array([0, 1, 1, 1, 2]), np.array([2, 3, 2, 4, 0]), np.array([3, 4, 5, 3, 2]), np.array([6, 5, 4, 4, 7])] fig, ax = plt.subplots(figsize=(12, 8))for X in datasets: μ = exp(X @ β) distribution = []for y_i in y_values: distribution.append(poisson_pmf(y_i, μ)) ax.plot(y_values, distribution, label=f'$\mu_i$={μ:.1}', marker='o', markersize=8, alpha=0.5) ax.grid() ax.legend() ax.set_xlabel('$y \mid x_i$') ax.set_ylabel(r'$f(y \mid x_i; \beta )$') ax.axis(xmin=0, ymin=0) plt.show()
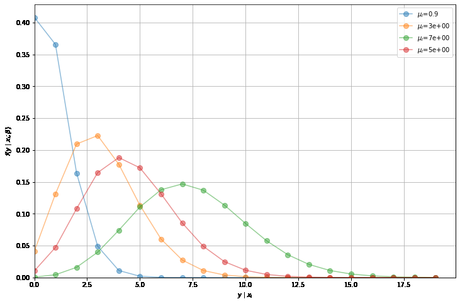
Podemos ver que la distribución de yi está condicionado a xi (μi ya no es constante).
Estimación de máxima verosimilitud
En nuestro modelo para el número de multimillonarios, la distribución condicional contiene 4 (k=4) parámetros que necesitamos estimar.
Etiquetaremos todo nuestro vector de parámetros como β dóndeβ=[β0β1β2β3]
Para estimar el modelo usando MLE, queremos maximizar la probabilidad de que nuestra estimación β^ es el verdadero parámetro β.
Intuitivamente, queremos encontrar el β^ que mejor se adapte a nuestros datos.
Primero, necesitamos construir la función de verosimilitud L(β), que es similar a una función de densidad de probabilidad conjunta.
Supongamos que tenemos algunos datos yi={y1,y2} y yi∼f(yi).
Si y1 y y2 son independientes, la PMF conjunta de estos datos es f(y1,y2)=f(y1)⋅f(y2).
Si yi sigue una distribución de Poisson con λ=7, podemos visualizar el PMF conjunto así
def plot_joint_poisson(μ=7, y_n=20): yi_values = np.arange(0, y_n, 1)# Create coordinate points of X and Y X, Y = np.meshgrid(yi_values, yi_values)# Multiply distributions together Z = poisson_pmf(X, μ) * poisson_pmf(Y, μ) fig = plt.figure(figsize=(12, 8)) ax = fig.add_subplot(111, projection='3d') ax.plot_surface(X, Y, Z.T, cmap='terrain', alpha=0.6) ax.scatter(X, Y, Z.T, color='black', alpha=0.5, linewidths=1) ax.set(xlabel='$y_1$', ylabel='$y_2$') ax.set_zlabel('$f(y_1, y_2)$', labelpad=10) plt.show() plot_joint_poisson(μ=7, y_n=20)
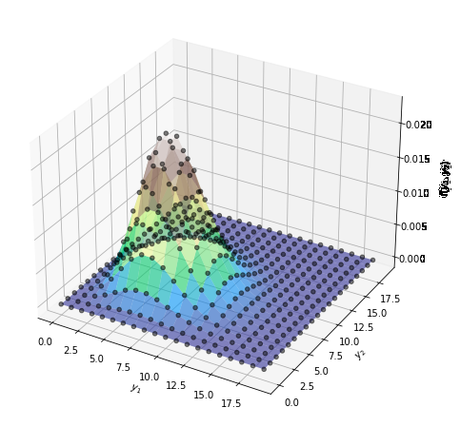
De manera similar, la pmf conjunta de nuestros datos (que se distribuye como una distribución condicional de Poisson) se puede escribir comof(y1,y2,...,yn∣x1,x2,...,xn;β)=∏i=1nμiyiyi!e−μi
yi está condicionado a ambos valores de xi y los parámetros β.
La función de verosimilitud es la misma que la pmf conjunta, pero trata el parámetro β como una variable aleatoria y toma las observaciones (yi,xi) como se indicaL(β∣y1,y2,...,yn ; x1,x2,...,xn)=∏i=1nμiyiyi!e−μi=f(y1,y2,...,yn∣ x1,x2,...,xn;β)
Ahora que tenemos nuestra función de verosimilitud, queremos encontrar el β^ que produce el valor de máxima verosimilitudmaxβL(β)
Al hacerlo, generalmente es más fácil maximizar la probabilidad logarítmica (considere diferenciar f(x)=xexp(x) vs. f(x)=log(x)+x).
Dado que tomar un logaritmo es una transformación creciente monótona, un maximizador de la función de verosimilitud también será un maximizador de la función logarítmica de verosimilitud.
En nuestro caso, la probabilidad logarítmica eslogL(β)= log(f(y1;β)⋅f(y2;β)⋅...⋅f(yn;β))=∑i=1nlogf(yi;β)=∑i=1nlog(μiyiyi!e−μi)=∑i=1nyilogμi−∑i=1nμi−∑i=1nlogy!
El MLE del Poisson al Poisson para β^ se puede obtener resolviendomaxβ(∑i=1nyilogμi−∑i=1nμi−∑i=1nlogy!)
Sin embargo, no existe una solución analítica para el problema anterior: para encontrar el MLE necesitamos usar métodos numéricos.
MLE con métodos numéricos
Muchas distribuciones no tienen buenas soluciones analíticas y, por lo tanto, requieren métodos numéricos para resolver las estimaciones de los parámetros.
Uno de esos métodos numéricos es el algoritmo de Newton-Raphson.
Nuestro objetivo es encontrar la estimación de máxima verosimilitud β^.
A β^, la primera derivada de la función logarítmica de verosimilitud será igual a 0.
Ilustremos esto suponiendologL(β)=−(β−10)2−10
β = np.linspace(1, 20)
logL = -(β - 10) ** 2 - 10
dlogL = -2 * β + 20
fig, (ax1, ax2) = plt.subplots(2, sharex=True, figsize=(12, 8)) ax1.plot(β, logL, lw=2) ax2.plot(β, dlogL, lw=2) ax1.set_ylabel(r'$log \mathcal{L(\beta)}$', rotation=0, labelpad=35, fontsize=15) ax2.set_ylabel(r'$\frac{dlog \mathcal{L(\beta)}}{d \beta}$ ', rotation=0, labelpad=35, fontsize=19) ax2.set_xlabel(r'$\beta$', fontsize=15) ax1.grid(), ax2.grid() plt.axhline(c='black') plt.show()
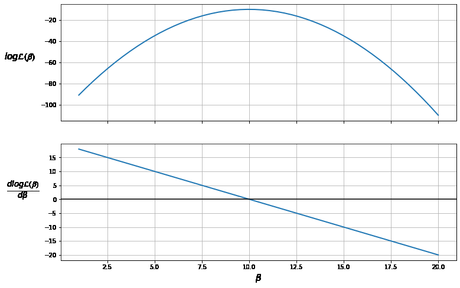
La gráfica muestra que el valor de máxima verosimilitud (la gráfica superior) ocurre cuando dlogL(β)dβ=0 (la trama inferior).
Por lo tanto, la probabilidad se maximiza cuando β=10.
También podemos asegurarnos de que este valor sea un máximo (en lugar de un mínimo) comprobando que la segunda derivada (pendiente del gráfico inferior) sea negativa.
El algoritmo de Newton-Raphson encuentra un punto donde la primera derivada es 0.
Para usar el algoritmo, hacemos una estimación inicial del valor máximo, β0 (las estimaciones de los parámetros de MCO pueden ser una suposición razonable), entonces
- Utilice la regla de actualización para iterar el algoritmoβ(k+1)=β(k)−H−1(β(k))G(β(k))dónde:G(β(k))=dlogL(β(k))dβ(k)H(β(k))=d2logL(β(k))dβ(k)dβ(k)′
- Compruebe si β(k+1)−β(k)<tol
- Si es verdadero, deje de iterar y configure β^=β(k+1)
- Si es falso, actualice β(k+1)
Como puede verse en la ecuación de actualización, β(k+1)=β(k) sólo cuando G(β(k))=0es decir. donde la primera derivada es igual a 0.
(En la práctica, dejamos de iterar cuando la diferencia está por debajo de un pequeño umbral de tolerancia)
Intentemos implementar el algoritmo de Newton-Raphson.
Primero, crearemos una clase llamada PoissonRegression para que podamos volver a calcular fácilmente los valores de probabilidad de registro, gradiente y hessiano para cada iteración.
class PoissonRegression:def __init__(self, y, X, β): self.X = X self.n, self.k = X.shape# Reshape y as a n_by_1 column vector self.y = y.reshape(self.n,1)# Reshape β as a k_by_1 column vector self.β = β.reshape(self.k,1)def μ(self):return np.exp(self.X @ self.β)def logL(self): y = self.y μ = self.μ()return np.sum(y * np.log(μ) - μ - np.log(factorial(y)))def G(self): y = self.y μ = self.μ()return X.T @ (y - μ)def H(self): X = self.X μ = self.μ()return -(X.T @ (μ * X))
Nuestra función newton_raphsontomará un PoissonRegression objeto que tiene una suposición inicial del vector de parámetrosβ0.
El algoritmo actualizará el vector de parámetros de acuerdo con la regla de actualización y volverá a calcular el gradiente y las matrices hessianas en las estimaciones de los nuevos parámetros.
La iteración terminará cuando:
- La diferencia entre el parámetro y el parámetro actualizado está por debajo de un nivel de tolerancia.
- Se ha alcanzado el número máximo de iteraciones (lo que significa que no se logra la convergencia).
Para que podamos tener una idea de lo que sucede mientras se ejecuta el algoritmo, display=True se agrega una opción para imprimir valores en cada iteración.
def newton_raphson(model, tol=1e-3, max_iter=1000, display=True): i = 0 error = 100# Initial error value# Print header of outputif display: header = f'{"Iteration_k":<13}{"Log-likelihood":<16}{"θ":<60}' print(header) print("-" * len(header))# While loop runs while any value in error is greater# than the tolerance until max iterations are reachedwhile np.any(error > tol) and i < max_iter: H, G = model.H(), model.G() β_new = model.β - (np.linalg.inv(H) @ G) error = β_new - model.β model.β = β_new# Print iterationsif display: β_list = [f'{t:.3}' for t in list(model.β.flatten())] update = f'{i:<13}{model.logL():<16.8}{β_list}' print(update) i += 1 print(f'Number of iterations:{i}') print(f'β_hat ={model.β.flatten()}')# Return a flat array for β (instead of a k_by_1 column vector)return model.β.flatten()
Probemos nuestro algoritmo con un pequeño conjunto de datos de 5 observaciones y 3 variables en X.
X = np.array([[1, 2, 5],
[1, 1, 3],
[1, 4, 2],
[1, 5, 2],
[1, 3, 1]])
y = np.array([1, 0, 1, 1, 0])
# Take a guess at initial βs init_β = np.array([0.1, 0.1, 0.1])# Create an object with Poisson model values poi = PoissonRegression(y, X, β=init_β)# Use newton_raphson to find the MLE β_hat = newton_raphson(poi, display=True)
Iteration_k Log-likelihood θ ----------------------------------------------------------------------------------------- 0 -4.3447622 ['-1.49', '0.265', '0.244'] 1 -3.5742413 ['-3.38', '0.528', '0.474'] 2 -3.3999526 ['-5.06', '0.782', '0.702'] 3 -3.3788646 ['-5.92', '0.909', '0.82'] 4 -3.3783559 ['-6.07', '0.933', '0.843'] 5 -3.3783555 ['-6.08', '0.933', '0.843'] Number of iterations: 6 β_hat = [-6.07848205 0.93340226 0.84329625]
Como se trataba de un modelo simple con pocas observaciones, el algoritmo logró la convergencia en solo 6 iteraciones.
Puede ver que con cada iteración, el valor de probabilidad logarítmica aumentó.
Recuerde, nuestro objetivo era maximizar la función de probabilidad logarítmica, que el algoritmo ha trabajado para lograr.
Además, tenga en cuenta que el aumento en logL(β(k)) se vuelve más pequeño con cada iteración.
Esto se debe a que el gradiente se acerca a 0 a medida que alcanzamos el máximo y, por lo tanto, el numerador de nuestra ecuación de actualización se hace más pequeño.
El vector de gradiente debe estar cerca de 0 en β^
poi.G()
array([[-3.95169228e-07],
[-1.00114805e-06],
[-7.73114562e-07]])
El proceso iterativo se puede visualizar en el siguiente diagrama, donde el máximo se encuentra en β=10
logL =lambda x: -(x - 10) ** 2 - 10def find_tangent(β, a=0.01): y1 = logL(β) y2 = logL(β+a) x = np.array([[β, 1], [β+a, 1]]) m, c = np.linalg.lstsq(x, np.array([y1, y2]), rcond=None)[0]return m, c β = np.linspace(2, 18) fig, ax = plt.subplots(figsize=(12, 8)) ax.plot(β, logL(β), lw=2, c='black')for β in [7, 8.5, 9.5, 10]: β_line = np.linspace(β-2, β+2) m, c = find_tangent(β) y = m * β_line + c ax.plot(β_line, y, '-', c='purple', alpha=0.8) ax.text(β+2.05, y[-1], f'$G({β}) = {abs(m):.0f}$', fontsize=12) ax.vlines(β, -24, logL(β), linestyles='--', alpha=0.5) ax.hlines(logL(β), 6, β, linestyles='--', alpha=0.5) ax.set(ylim=(-24, -4), xlim=(6, 13)) ax.set_xlabel(r'$\beta$', fontsize=15) ax.set_ylabel(r'$log \mathcal{L(\beta)}$', rotation=0, labelpad=25, fontsize=15) ax.grid(alpha=0.3) plt.show()
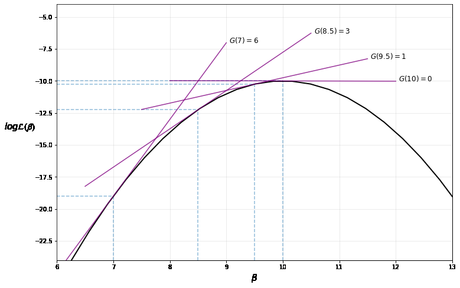
Tenga en cuenta que nuestra implementación del algoritmo de Newton-Raphson es bastante básica; para implementaciones más sólidas, consulte, por ejemplo, scipy.optimize .
Estimación de máxima verosimilitud con statsmodels
Ahora que sabemos lo que está pasando bajo el capó, podemos aplicar MLE a una aplicación interesante.
Usaremos el modelo de regresión de Poisson statsmodels para obtener una salida más rica con errores estándar, valores de prueba y más.
statsmodels utiliza el mismo algoritmo anterior para encontrar las estimaciones de máxima verosimilitud.
Antes de comenzar, volvamos a estimar nuestro modelo simple con statsmodels para confirmar que obtenemos los mismos coeficientes y valor logarítmico de verosimilitud.
X = np.array([[1, 2, 5],
[1, 1, 3],
[1, 4, 2],
[1, 5, 2],
[1, 3, 1]])
y = np.array([1, 0, 1, 1, 0])
stats_poisson = Poisson(y, X).fit()
print(stats_poisson.summary())
Optimization terminated successfully.
Current function value: 0.675671
Iterations 7
Poisson Regression Results
==============================================================================
Dep. Variable: y No. Observations: 5
Model: Poisson Df Residuals: 2
Method: MLE Df Model: 2
Date: Thu, 15 Jul 2021 Pseudo R-squ.: 0.2546
Time: 00:14:01 Log-Likelihood: -3.3784
converged: True LL-Null: -4.5325
Covariance Type: nonrobust LLR p-value: 0.3153
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -6.0785 5.279 -1.151 0.250 -16.425 4.268
x1 0.9334 0.829 1.126 0.260 -0.691 2.558
x2 0.8433 0.798 1.057 0.291 -0.720 2.407
==============================================================================
Ahora repliquemos los resultados del artículo de Daniel Treisman, Los multimillonarios de Rusia , mencionado anteriormente en la conferencia.
Treisman comienza estimando la ecuación (58.1) , donde:
- yi es number of billionairesi
- xi1 es logGDP per capitai
- xi2 es logpopulationi
- xi3 es years in GATTi - años de membresía en el GATT y la OMC (para poder acceder a los mercados internacionales)
El documento solo considera el año 2008 para la estimación.
Configuraremos nuestras variables para la estimación de esa manera (debe tener los datos asignados df desde antes en la lección)
# Keep only year 2008 df = df[df['year'] == 2008]# Add a constant df['const'] = 1# Variable sets reg1 = ['const', 'lngdppc', 'lnpop', 'gattwto08'] reg2 = ['const', 'lngdppc', 'lnpop', 'gattwto08', 'lnmcap08', 'rintr', 'topint08'] reg3 = ['const', 'lngdppc', 'lnpop', 'gattwto08', 'lnmcap08', 'rintr', 'topint08', 'nrrents', 'roflaw']
Entonces podemos usar la Poissonfunción de statsmodels para ajustar el modelo.
Usaremos errores estándar robustos como en el artículo del autor.
# Specify model poisson_reg = sm.Poisson(df[['numbil0']], df[reg1], missing='drop').fit(cov_type='HC0') print(poisson_reg.summary())
Optimization terminated successfully.
Current function value: 2.226090
Iterations 9
Poisson Regression Results
==============================================================================
Dep. Variable: numbil0 No. Observations: 197
Model: Poisson Df Residuals: 193
Method: MLE Df Model: 3
Date: Thu, 15 Jul 2021 Pseudo R-squ.: 0.8574
Time: 00:14:01 Log-Likelihood: -438.54
converged: True LL-Null: -3074.7
Covariance Type: HC0 LLR p-value: 0.000
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -29.0495 2.578 -11.268 0.000 -34.103 -23.997
lngdppc 1.0839 0.138 7.834 0.000 0.813 1.355
lnpop 1.1714 0.097 12.024 0.000 0.980 1.362
gattwto08 0.0060 0.007 0.868 0.386 -0.008 0.019
==============================================================================
¡Éxito! El algoritmo pudo lograr la convergencia en 9 iteraciones.
Nuestro resultado indica que el PIB per cápita, la población y los años de membresía en el Acuerdo General sobre Aranceles Aduaneros y Comercio (GATT) están relacionados positivamente con la cantidad de multimillonarios que tiene un país, como se esperaba.
Estimemos también los modelos más completos del autor y los mostraremos en una sola tabla.
regs = [reg1, reg2, reg3]
reg_names = ['Model 1', 'Model 2', 'Model 3']
info_dict = {'Pseudo R-squared':lambda x: f"{x.prsquared:.2f}", 'No. observations':lambda x: f"{int(x.nobs):d}"} regressor_order = ['const', 'lngdppc', 'lnpop', 'gattwto08', 'lnmcap08', 'rintr', 'topint08', 'nrrents', 'roflaw'] results = []for reg in regs: result = sm.Poisson(df[['numbil0']], df[reg], missing='drop').fit(cov_type='HC0', maxiter=100, disp=0) results.append(result) results_table = summary_col(results=results, float_format='%0.3f', stars=True, model_names=reg_names, info_dict=info_dict, regressor_order=regressor_order) results_table.add_title('Table 1 - Explaining the Number of Billionaires\ in 2008') print(results_table)
Table 1 - Explaining the Number of Billionaires in 2008
=================================================
Model 1 Model 2 Model 3
-------------------------------------------------
const -29.050*** -19.444*** -20.858***
(2.578) (4.820) (4.255)
lngdppc 1.084*** 0.717*** 0.737***
(0.138) (0.244) (0.233)
lnpop 1.171*** 0.806*** 0.929***
(0.097) (0.213) (0.195)
gattwto08 0.006 0.007 0.004
(0.007) (0.006) (0.006)
lnmcap08 0.399** 0.286*
(0.172) (0.167)
rintr -0.010 -0.009
(0.010) (0.010)
topint08 -0.051*** -0.058***
(0.011) (0.012)
nrrents -0.005
(0.010)
roflaw 0.203
(0.372)
Pseudo R-squared 0.86 0.90 0.90
No. observations 197 131 131
=================================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01
El resultado sugiere que la frecuencia de multimillonarios se correlaciona positivamente con el PIB per cápita, el tamaño de la población, la capitalización del mercado de valores y se correlaciona negativamente con la tasa de impuesto sobre la renta marginal máxima.
Para analizar nuestros resultados por país, podemos trazar la diferencia entre los valores predichos y reales, luego ordenar de mayor a menor y trazar los primeros 15
data = ['const', 'lngdppc', 'lnpop', 'gattwto08', 'lnmcap08', 'rintr',
'topint08', 'nrrents', 'roflaw', 'numbil0', 'country']
results_df = df[data].dropna()
# Use last model (model 3) results_df['prediction'] = results[-1].predict()# Calculate difference results_df['difference'] = results_df['numbil0'] - results_df['prediction']# Sort in descending order results_df.sort_values('difference', ascending=False, inplace=True)# Plot the first 15 data points results_df[:15].plot('country', 'difference', kind='bar', figsize=(12,8), legend=False) plt.ylabel('Number of billionaires above predicted level') plt.xlabel('Country') plt.show()
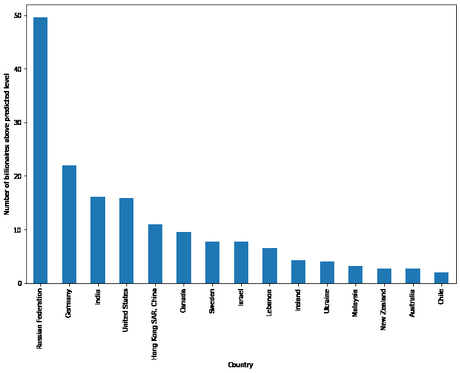
Como podemos ver, Rusia tiene, con mucho, el mayor número de multimillonarios por encima de lo que predice el modelo (alrededor de 50 más de lo esperado).
Treisman usa este resultado empírico para discutir las posibles razones del exceso de multimillonarios de Rusia, incluido el origen de la riqueza en Rusia, el clima político y la historia de la privatización en los años posteriores a la URSS.

