Estrellas y Polígonos estrellados

Con carácter general, una estrella, como objeto matemático, no está definido de forma unívoca. Existen grafos estrellados, polígonos estrellados, estrellas o formas estrelladas... y todos ellos tienen definiciones que a veces se solapan o se refieren indistintamente a uno u otro objeto.
Las estrellas aparecen en la naturaleza (estrellas de mar, flores), la religión (pentagrama, estrella de David), el arte (en arquitectura las estrellas se han usado para rosetones en catedrales, edificios, motivos ornamentales, etc...), pero también aparecen en logotipos de muchas marcas comerciales y por ejemplo en las banderas de muchos países, esto hace que su estudio a la vez que interesante, resulte divertido.
Desde el punto de vista matemático, de las formas estrelladas o estrellas nos interesan fundamentalmente los polígonos estrellados y las estrellas.
Polígonos estrellados y estrellas.
A partir de un polígono regular de n lados se pueden construir formas estrelladas, que se clasifican en dos categorías: polígonos estrellados y estrellas.
Para construirlos se unen los vértices del polígono regular “avanzando” p vértices en cada paso. En el caso de que n y p sean primos entre sí, todos los vértices resultan unidos y se obtiene un polígono estrellado que se denota por n/p (notación de Schäfli).
Por ejemplo en el caso del pentágono regular se obtiene el polígono estrellado también llamado Pentagrama que se escribiría usando la notación de Schäfli 5/2. Éste poligono era el famoso símbolo de los Pitagóricos.

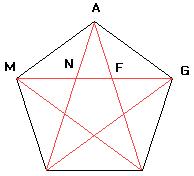
Polígono estrellado 5/2

Si consideramos el polígono regular de 7 lados tenemos dos números que son primos con 7, (basta considerar hasta la mitad del número de lados porque los otros casos son simétricos). Estos son el 2 y el 3,  mcd (2,7) = 1 y mcd (3,7) = 1

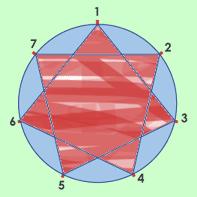
Polígono estrellado 7/2

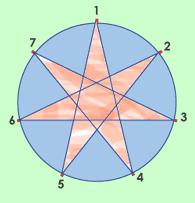
Polígono estrellado 7/3

Si consideramos el polígono de 8 lados, tenemos un único número que es primo con 8 y es menor que 4, estamos hablando del 3. Entonces uniendo vértices de 3 en 3 nos aparecen este polígono estrellado.

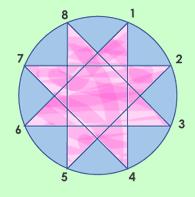
Polígono estrellado 8/3

Cuando n y p no son primos entre sí, todos los vértices del polígono inicial no pueden unirse y lo que se obtiene es una figura formada por varios polígonos entrelazados, que se llama estrella.

Estrella de 6/2          

La estrella 6/2 también conocida como hexagrama, estrella de David o símbolo de Salomón está formada por dos triángulos equiláteros girados 60º uno con respecto a otro.
  

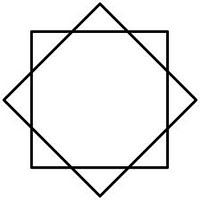
Estrella 8/2

 La estrella 6/2 también conocida como hexagrama está formada por dos cuadrados girados 45º uno con respecto a otro.
 


Polígonos estrellados que se forman al prolongar los lados del polígono
También a partir de un polígono de n vértices podemos construir formas estrelladas de la siguiente forma:
Un vez dibujado el polígono se prolongan los lados hasta que sus prolongaciones se corten por primera vez, obteniéndose la primera forma estrellada denotado por n/2.
Si continuamos prolongando los lados del polígono se cortarán por segunda vez determinando una nueva forma que denotaremos por n/3
Así sucesivamente podemos formar todos los polígonos estrellados o estrellas posibles a partir de un polígono. Veamos algunos ejemplos:

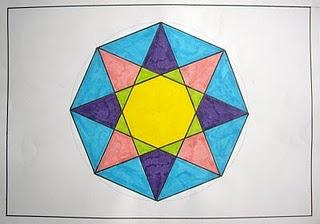
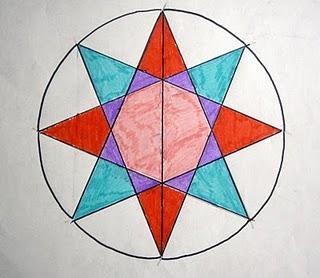
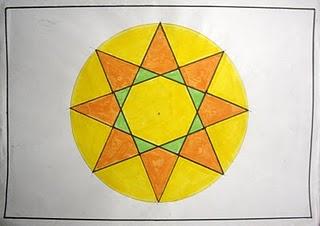
Polígonos cóncavos con forma de estrella
Conectando los 2n segmentos que forman el contorno de una estrella n/q se construye un polígono cóncavo que se denota por [n/q]

Estrella de 5 puntas. 10 lados

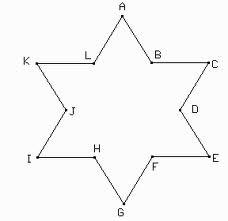
Estrella de 6 puntas. 12 lados

Estrella de 8 puntas. 16 lados

Presencia de las estrellas en la vida cotidiana.
Las estrellas, como decíamos al principio tienen una presencia bastante frecuente en el arte, el diseño, la naturaleza, el religión, pero también se pueden convertir en un buen recurso didáctico para las clases de matemáticas. Veamos algunos ejemplos:
Logotipos, marcas comerciales, banderas:

Logotipo

Marca comercial

En la religión:

Estrella de David

La estrella tartésica está en la mitología y la religiosidad tartésica adoradora del sol, y los andaluces están unidos al astro rey desde el principio de los tiempos. Por eso, muchos consideran a la estrella tartésica como el símbolo de Andalucía.

Estrella tartésica

La cruz de Malta. La estrella tiene ocho puntas que representan los ocho países de procedencia de los caballeros pero también las ocho virtudes que defendían: Verdad, fe, arrepentimiento,humildad, justicia, misericordia, pureza y soportación de las persecuciones.

En la naturaleza:

Estrella de mar

Forma pentagonal

Las estrellas usadas como recuso en clase de matemáticas.
El juego de las damas chinas:

Estrellas mágicas:

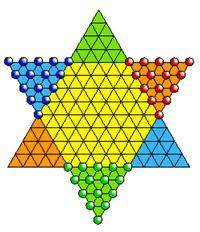
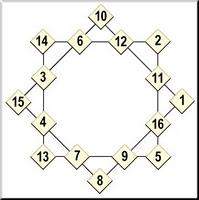
Juego en la estrella Tartésica en Matesy+   Ver
Por último una curiosidad: En la Edad Media, los maestros constructores firmaban sus obras con marcas de cantería. Algunas veces están hechas sobre polígonos estrellados.