Fascinantes historias de la ciencia - 3: El triángulo egipcio

Pitágoras observaba a los agrimesores egipcios afanarse con sus cuerdas entre los campos enlodados. Iban cargados con estacas y las clavaban con gran precisión en los puntos que indicaban sus tablillas. Lo hacían con gran pericia y solo utilizaban una larga cuerda con nudos equidistantes. Después de trazar cada parcela aplicaban a los postes los sellos imperiales y un escriba grababa los signos de cada agricultor. Las parcelas asignadas estaban perfectamente medidas pese a que la crecida del Nilo convertía las tierras negras en un lodazal. Los agricultores esperaban pacientemente que terminaran para hacerse cargo de su parcela y empezar las tareas de siembra.

Pitágoras se acercó a los funcionarios. Enseguida se dio cuenta de que la cuerda que utilizaban estaba dividida en 12 partes iguales marcadas con nudos. El sacerdote que los dirigía, que había estudiado en las escuelas de los templos  conocía los secretos de la medida y el cálculo, ahora oficiaba de funcionario real para repartir las parcelas de tierra tras la crecida anual. Sus ayudantes estaban trabajando con una cuerda ya preparada, pero esta terminó por romperse al estirarla fuertemente cuando clavaban una estaca. El sacerdote no se inmutó. Cogió un trozo de cuerda de lino nueva sin nudo alguno y se preparó para dividirla en 12 partes. El griego observó con curiosidad. El sacerdote egipcio la unió formando una línea cerrada y la dobló primero en 4 partes iguales con ayuda de una caña clavada en el suelo a la que rodeaba uno de los extremos. Después clavó una segunda caña al lado de la primera y pasó la cuerda por detrás mientras tiraba con una mano de las cuerdas que quedaban entre las cañas y con la otra del cabo que quedaba libre. Ajustó la tensión hasta que ambos extremos quedaron a la misma distancia: así obtenía tres trozos iguales con 4 cuerdas cada uno. Aplicó después una marca de pintura roja en los tres extremos obtenidos asegurándose de que se marcaban bien las 4 cuerdas de que constaban. Ya tenia un nuevo instrumento para continuar con las medidas ese día. 

Pitágoras seguía con curiosidad las maniobras de los ayudantes: Clavaban una estaca en la tierra húmeda en lo que sería la esquina de una de las parcelas, luego estiraban la cuerda para formar un triángulo dejando a cada lado 3 y 4 espacios respectivamente. El otro lado del triángulo quedaba formado  por 5 nudos pero, pero no era eso lo que les interesaba en ese momento. Así, con extraordinaria facilidad y exactitud formaban un ángulo recto al que prolongaban los lados la distancia necesaria hasta alcanzar la longitud de la parcela asignada por el faraón. 

Pitágoras decidió hablar con el sacerdote. Se presentó como viajero griego interesado en las matemáticas y alabó sus trabajo y sus conocimientos. Después le invitó a las tabernas cercanas al Nilo donde el vino y la cerveza, pagados a su costa, desatarían su lengua. Así se enteró de que los egipcios conocían muy bien las propiedades de ese triángulo que manejaban con tanta facilidad. Le llamaban triángulo de Isis

y tenía para ellos carácter sagrado. El sacerdote le confesó que este triángulo era la esencia del mundo. Era además el símbolo de la fecundidad: el lado vertical simbolizaba el macho, la base la hembra y la hipotenusa la primogenitura de los dos.  Pitágoras se cuidó muy mucho de expresar la opinión que le merecían estas últimas revelaciones pues los griegos consideraban que la forma más perfecta era la esfera y, por supuesto, las relaciones de las figuras matemáticas con la fecundidad le parecían ridículas; pero hubo de reconocer admirado que sus pirámides eran asombrosas y -le según le había revelado al oído el sacerdote- todas tenías incorporado en alguna de sus dimensiones el triángulo sagrado. 
Aquel encuentro desató su curiosidad. La facilidad con que los egipcios lograban fabricar  una escuadra con números tan sencillos, consecutivos además, le parecía muy interesante. El ángulo recto estaba presente en todo cuanto le rodeaba: en el corte de la plomada con el estanque, en la posición de la pared sobre el suelo, en la figura de los árboles elevándose hacia el cielo, en la verticalidad de la caída de una piedra sobre el patio, en los quicios de las puertas, en las esquinas de las casas, en los radios de las ruedas con los ejes... este ángulo parecía tener suma importancia. Los egipcios empleaban para construirlo una terna simple de medidas: 3, 4 y 5. Se preguntó si habría más ternas que también cumplieran ese objetivo. Evidentemente sus dobles, sus triples y cualquier múltiplo de los tres los cumplía también. 6, 8 y 10; 9, 12 y 15... ¿Acaso habría alguna con números no relacionados mediante multiplicación de la terna? Tras algunas pruebas encontró una terna no proporcional a la primitiva y bastante sencilla: 5, 12 y 13. 

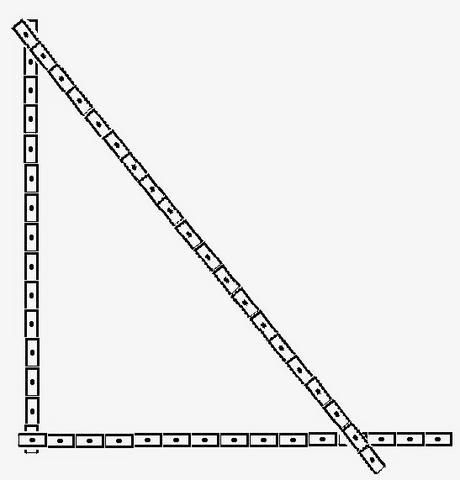
Había estado aguas arriba del Nilo  una temporada pero debía regresar a Alejandría. Pensó en plantear este problema a otros estudiosos de la biblioteca y, efectivamente, puestos a la labor aparecieron otras ternas que también cumplían la condición de formar un ángulo recto. Trabajaron con palillos iguales hasta obtener una considerable cantidad de triángulos rectángulos. Incluso idearon un artilugio, de bastante precisión, mediante listones perforados con 100 agujeros equidistantes. Dos de ellos fijos en escuadra por uno de sus extremos y el otro libre para ir probando en qué posiciones podrían encajar los agujeros en los dos ejes.  Así ampliaron las ternas hasta 16 de ellas: 

( 3 , 4 , 5 ) ( 5, 12, 13) ( 7, 24, 25) ( 8, 15, 17)( 9, 40, 41) (11, 60, 61) (12, 35, 37) (13, 84, 85)(16, 63, 65) (20, 21, 29) (28, 45, 53) (33, 56, 65)(36, 77, 85) (39, 80, 89) (48, 55, 73) (65, 72, 97)

Pitágoras pensó en darse por satisfecho con los resultados obtenidos. Intuía que estos números guardaban algún secreto, que obedecían a alguna ley matemática; pero no lograba encontrar fórmula alguna para relacionarlos. Estaba sumido en estos pensamientos cuando un colega vino a informarle de que habían encontrado algunos papiros con traducciones babilónicas que parecían tratar de este problemas. Los babilónicos escribían en tablillas de arcilla y su escritura era completamente diferente. Aquella escritura ya no se podía traducir y, además quedaban muy pocas tablillas, aunque la biblioteca las guardaba con la esperanza de poder hacerlo algún día. Sin embargo, se había logrado recopilar antiguas obras con parte de sus conocimientos y sus avances matemáticos les habían desconcertado. Entre los apuntes dejados por antiguos expertos en esa cultura destacaba su efectivo sistema de numeración, sus conocimientos de álgebra, de las fracciones, potencias... y, lo más sorprendente, aparecían ya las ternas que tan laboriosamente habían encontrado ¡y ampliadas hasta 38! Según parecía incluso encontraron asombrosas relaciones entre los lados. Si hubieran dispuesto de aquellas tablillas y un traductor quizás sabrían qué relación guardaban aquellos números. 

Tablilla babilónico-sumeria PLIMPTON 322
Pitágoras se resignó. Le embargaba una leve melancolía mientras jugueteaba con las pequeñas piezas de cerámica cuadradas que servían de fichas en los juegos de mesa. Se le ocurrió alinearlos formando el triángulo de Isis.  Por un instante pensó que aquellos cuadradaditos que se cerraban en el borde del triángulo sagrado parecían tres frentes de falanges macedónicas a punto de enfrentarse. Aquellas formaciones cuadradas que Alejandro Magno paseó triunfales por el mundo. Se entretuvo en formar con sus fichas unas falanges en miniatura, cada una adecuada al tamaño de cada lado. Sería una batalla igualada, pensó. De pronto el destello de una idea sacudió su mente. ¡Ahí estaba la solución! La suma de los cuadrados de los  lados menores era igual que el cuadrado del lado mayor. Excitado se lanzó a comprobarlo con cada una de las ternas conocidas: todas ellas cumplían la igualdad. Probó entonces con triángulos rectángulos al azar: aquella ley se cumplía aun cuando los lados obtenidos contuvieran decimales. Había dado con un principio matemático extraordinario. En los días siguientes estuvo trabajando en las posibilidades de aquel descubrimiento. Las consecuencias de aquel teorema abrían un campo apasionante al cálculo matemático. Pronto la trigonometría se desarrollaría como una herramienta fundamental para el avance de las matemáticas. Y todo gracias al triángulo de Isis.

NOTA: El relato recrea en versión libre y con numerosas licencias narrativas como pudo producirse el descubrimiento del famoso Teorema de Pitágoras. Sirva como ofrenda  de apaciguamiento al Dios de las Matemáticas al que de joven ofendí en tantas ocasiones. Uno de los momentos en que los insultos fueron más gruesos ocurrió cuando tuve que aprender, sin entenderlo, esta igualdad que se me hacía completamente inútil.  Cuando llegué a comprender esta sencilla igualdad e investigué la historia de su descubrimiento quedé fascinado por sus connotaciones: resulta que antiquísimas civilizaciones, como la de Mesopotamia, lo conocían, los chinos lo habían dibujado y los egipcios e hindúes lo aplicaban, aún sin saber su constancia universal, en las medidas y construcciones de sus templos. 

De su conocimiento por los babilónicos existen pruebas documentales irrefutables basadas en varias tablillas (Tablilla YALE o YBC 7289) y, sobre todo, en la completísima tablilla PLIMPTON 322 (datada en un milenio anterior a Pitágoras) donde se establecen relaciones matemáticas complejas entre los elementos de un triángulo rectángulo (entre ellas el propio teorema, pero también otras relaciones trigonométricas)
De los chinos se sabe de la existencia de una demostración publicada en la obra matemática Chou Pei, pudiendo ser ésta anterior a Pitágoras, aunque se cree que este no llegó a conocer esta obra.