Forma y sonido según Gravedad Cuántica

01:36:00 | | Editar entrada Las matemáticas son, en esencia, una lengua artificial para articular con precisión las teorías sobre el mundo físico. A diferencia de lenguaje natural, sin embargo, la traducción de las diferentes clases de matemáticas puede ser difícil en el mejor de los casos. Tal es el encontrado en el intento de unificar la relatividad general y la teoría cuántica, ya que se expresan en la geometría diferencial y el análisis funcional, respectivamente. Dicho esto, la geometría espectral - un campo de las matemáticas que se refiere a las relaciones entre las estructuras geométricas de los colectores y los espectros de los operadores diferenciales canónicamente definido - se puede resolver este dilema desde hace mucho tiempo por lo que el espacio-tiempo a tratar como al mismo tiempo continuo y discreto, esencialmente en relación a la frecuencia sonido basada en el tejido del espacio-tiempo a su forma base múltiple. Recientemente, los científicos del Instituto de Tecnología de California, la Universidad de Princeton, la Universidad de Waterloo, y la Universidad de Queensland normalizaron y segmentaron en pasos pequeños la geometría espectral, de dimensión finita. A continuación, demostraron su enfoque de cálculo de las formas de los objetos bidimensionales a partir de sus espectros de vibración como viable en dos, y posiblemente más, dimensiones.
El Prof. Achim Kempf analiza la investigación que él, David Aasen, Tejal Bhamre cabo. "Antes de que los nuevos resultados", dice Kempf Phys.org, se pensó "que la geometría espectral es demasiado lineal - y por lo tanto simplemente demasiado difícil de usar -. Con el propósito de unificar la relatividad general y la teoría cuántica En el nuevo documento, sin embargo, hemos demostrado que la geometría espectral puede ser domesticada y convertida en un método práctico de gran utilidad, a saber adecuadamente cortándola en pequeños, y por lo tanto manejable, piezas lineales".

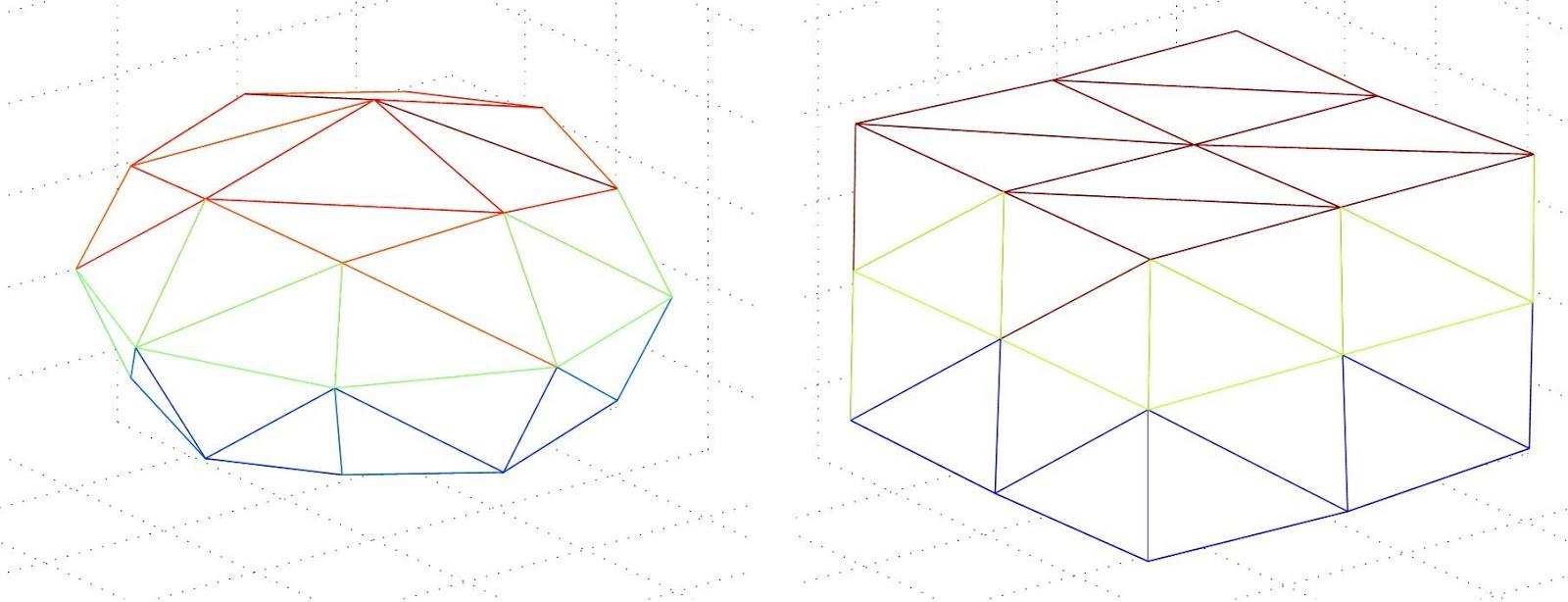
Instantáneas del algoritmo a partir de una esfera y el cubo de la búsqueda de su espectro solo. Cortesía y reconocimiento Achim Kempf. Derechos de autor 2013 por The American Physical Society

Kempf toma nota de que, en casos especiales, la geometría espectral tiene ciertas ambigüedades: matemáticas, como formas curvas especiales de grandes dimensiones que tienen el mismo espectro - es decir, sonarían igual de las que podríamos detectar en las dimensiones superiores. "La preocupación ha sido que si había demasiados tales ambigüedades también en nuestro mundo tridimensional, esto podría hacer la geometría espectral impráctica como herramienta en la física", explica Kempf. "En el nuevo estudio puso de manifiesto que, por suerte, los pequeños linealizados pasos que tomamos son, casi siempre, libres de ambigüedad -. Y durante dos formas tridimensionales en tres dimensiones, no hemos podido encontrar ambigüedades en absoluto relación con esto, sería muy interesante para extender la geometría espectral de una descripción del espacio en cada momento a una descripción unificada de espacio y tiempo. Esto todavía necesita un mayor desarrollo. " 
Dicho esto, Kempf señala que su idea – abordar problemas de geometría espectral y ambigüedades de la regularización y la segmentación de la geometría espectral en pasos de dimensión finita – funciona muy bien. "El tiempo de cálculo puede ser un poco largo", señala, pero creemos que vamos a ser capaces de acelerar significativamente los cálculos. Nos gustaría ser capaces de ejecutarlos, por ejemplo, en un teléfono inteligente”. 
Una sola idea clave permitió a los investigadores abordar estos desafíos de dos maneras. Esencialmente, en la medida que se refiere a la matemática, el problema fue encontrar un método que permitiría a uno calcular la forma de un objeto a partir del sonido que hace al vibrar. "Con este fin, la clave de visión era que este problema geométrico espectral, a pesar de ser altamente no lineal, puede en realidad ser domesticado con nuestra estrategia, que tiene dos componentes," explica Kempf. "En primer lugar, hacer los cálculos no lineales manejables cortándolos en pequeños pasos factibles." En la práctica, se observa que el ordenador hace esto comenzando con un poco de forma aleatoria, tal como la forma de una esfera. Entonces, mientras se mantiene comparando el sonido de la esfera con el sonido del objeto que se tiene que identificar, el equipo va a cambiar la forma de la esfera hasta que llega a la forma del objeto que tenía que identificar. 
"El segundo paso es regularizar - es decir, no tratar de obtener todos los detalles de la forma a la vez", dice Kempf. "En cambio, el cálculo de la forma aproximada de sólo una parte del espectro de sonido." Para entonces gradualmente el uso de más del espectro de sonido, este enfoque permite que especifiquen la forma con precisión cada vez mayor. 
"La belleza de nuestra nueva geometría espectral es que nos permite describir la forma de un jarrón, o, finalmente, la forma de la tela del espacio-tiempo, a través de los llamados invariantes - es decir, por las cantidades que no dependen de ninguna elección de sistema de coordenadas ", añade Kempf. "Esto es importante porque si queremos desarrollar una teoría que unifica la teoría cuántica y la relatividad general, cantidades importantes fundamentalmente no pueden depender de decisiones hechas por el hombre, como qué sistema de coordenadas que se quiera utilizar." 
Kempf entonces resume la relación de su enfoque, que ofrece una identificación, independiente de indicadores, de los títulos de la métrica de la libertad en términos de invariantes que deben estar dispuestos a cuantificar, con varios intentos matemáticos para unificar la relatividad general y la teoría cuántica.

• Bucle gravedad cuántica y la teoría de cuerdas: "Los nuevos métodos geométricos espectrales están profundamente relacionadas con la generalizados principios de incertidumbre de Heisenberg - y, de hecho, el nuevo trabajo surgió a partir de los estudios de estos principios, que han demostrado estar relacionada con la gravedad cuántica de bucles, así en cuanto a la teoría de cuerdas por mí y con la colaboración de Martin Bojowald".
• Series causales: "Tal vez, pero no está claro si hay una conexión"
• E8 propuesta de Garrett Lisi: "Probablemente no hay conexión"
• Geometría no conmutativa: "Programa de geometría no conmutativa de Alain Connes muestra que los espacios curvos pueden ser descritos por un espectral triple, que incluye el espectro del operador de Dirac No está claro si el espectro del operador de Dirac por sí sola es suficiente para calcular la forma de. un espacio curvo. Los nuevos métodos geométricos espectrales que presentamos aquí se puede utilizar para explorar esta interesante pregunta más otra, y de hecho estamos trabajando en esto"
• Supergravity: "Nuestros nuevos resultados se aplican a la gravedad y no requieren la supersimetría Esto es bueno porque todavía no hay evidencia sólida de que existe la supersimetría en la naturaleza".
• Modelos Twistor: "No hay conexión conocida"

En el futuro, dice Kempf, los científicos están trabajando en la generalización de los nuevos métodos a las formas que se curvan en el espacio y el tiempo, ya que entonces será útil para abordar algunas de las cuestiones fundamentales de la cosmología - incluida la cuestión de cómo empezó todo. "Más específicamente, Kempf añade que, si bien las fluctuaciones cuánticas son hoy en día casi infinitamente pequeño, se cree que el espacio-tiempo en sí surgió de una especie de salto cuántico." Nuestros resultados nos llevan un paso más cerca de ser capaz de calcular explícitamente el timbre cuántica del espacio-tiempo, que a su vez podría decirnos más sobre el origen de nuestro universo".
En cuanto a las otras áreas de investigación que podrían beneficiarse de su estudio, puntos Kempf señala que los experimentadores aún tienen un largo camino por recorrer para medir directamente los efectos de gravedad cuántica. "Sin embargo", añade, "los nuevos métodos también se pueden utilizar para programar un ordenador con el fin de calcular la forma de los objetos por su sonido. Además", concluye, "estamos planeando mejorar nuestro algoritmo para que sea mucho más rápido; esto podría abrir aplicaciones de ingeniería, por ejemplo, permitiría desarrollar equipos para identificar rápidamente las formas a partir de una huella espectral simple"
Referencia:

• Princeton Journal Watch
• Physical Review
• Arxiv.org