Funciones, Derivadas Problema resuelto

Aprendiendo matemáticas con ejercicios propuestos por ustedes

Problema

Problema
El departamento de investigación de fragancias para mujeres "Las Bonitas" observa que cuando sus perfumes se venden a \(\$\)200 cada uno se venden 100 al mes. Sin embargo cuando el precio sube a \(\$\)250, solo se venden 50 al mes. Suponiendo que la demanda es lineal ¿A que precio se deben vender para obtener los ingresos máximos?

Solución 1:

Sabemos que la ecuación de una recta es:
\( \cfrac{Y-y_{0}}{X-x_{0}}=m \quad ...(i) \)
donde:
\(m\): es la pendiente de la recta, es un valor constante, nos indica cuan empinada es una recta.
\((x_{0},y_{0})\): es un punto de la recta, como se aprecia en el gráfico de abajo.

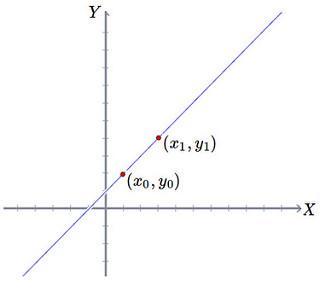
Podemos generalizar \((i)\) para dos puntos en la recta.
\( \cfrac{Y-y_{0}}{X-x_{0}} =\cfrac{Y-y_{1}}{X-x_{1}} \quad ...(ii) \)
Utilizando la propiedad aritmética:
\( \cfrac{a}{b}=\cfrac{c}{d}=\cfrac{a-c}{b-d} \)
En \((ii)\):
\( \cfrac{Y-y_{0}}{X-x_{0}} =\cfrac{Y-y_{1}}{X-x_{1}}=\cfrac{y_{1}-y_{0}}{x_{1}-x_{0}} \quad ...(iii) \)
Si asumimos que el eje \(Y\) represente el \( \textrm{precio del perfume}\) y el eje \(X\) la \( \textrm{cantidad de perfumes vendidos}\) y dado que tienen una relación lineal, entonces el par ordenado \( (\textrm{precio del perfume},\textrm{la cantidad de perfumes vendidos})\) es un punto que pertenece a una recta.
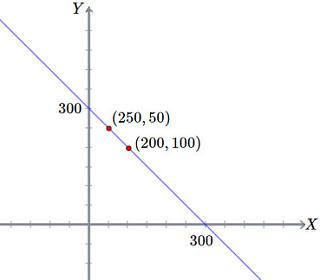
Del enunciado se identifican 2 puntos:
\( (x_{0},y_{0}) = (200,100) \)
\( (x_{1},y_{1}) = (250,50) \)
Reemplazando en \((iii)\), tenemos:
\( \cfrac{Y-200}{X-100} =\cfrac{Y-250}{X-50}=\cfrac{50}{-50}=-1 \\ \rightarrow Y = -X + 300 \quad ...(iv) \)
Es decir:

La ganancia, \(G_{(x)}\), viene dada por:
\( G_{(x)}= (\textrm{precio del perfume}) \times (\textrm{cantidad de perfumes vendidos}) \)
\( G_{(x)}= (x) (y) \)
\( G_{(x)}= (x) (-x+300) \\ \rightarrow G_{(x)}= -x^2+300x \quad ...(v) \)
Queremos encontrar con que valor de \(x\) la función \(G_{(x)}\) alcanza su valor más grande, una forma de hacer ello es derivar la función \(G_{(x)}\) respecto a \(x\) e igualar a cero, es decir
\( \cfrac{\mathrm{d}G_{(x)}}{\mathrm{d}x}=0 \\ \rightarrow \cfrac{\mathrm{d}}{\mathrm{d}x}(-x^2+300x)=0 \\ \rightarrow -2x+300 = 0 \\ \rightarrow x = 150 \)
Nota
La segunda derivada de \(G\), es decir \(G''\), resulta -2 esto comprueba que el valor de \(x\) maximiza la función G.