Graficando ecuaciones polares en MATLAB con Octave UPM

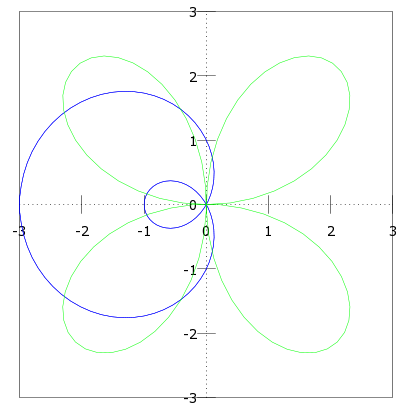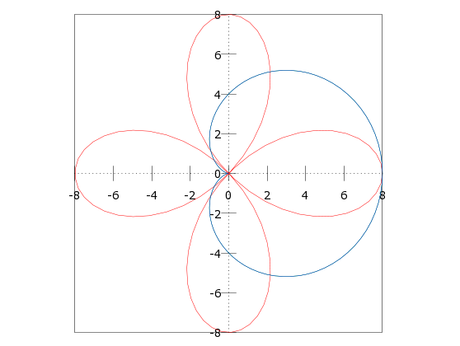
En esta entrada vamos a graficar algunas ecuaciones polares como las rectas, circunferencias, limazones con rizo, cardiodes, limazones con hendidura, limazones convexos, lemniscatas, rosas y espirales utilizando MATLAB y Octave UPM.
En primer lugar debemos tener descargado Octave UPM. Sí no sabes que es Octave UPM te invito a pasar por la entrada Aprendiendo MATLAB con Octave UPM donde verás como descargarlo y algunas nociones básicas que te serán de utilidad. 
Sí bien existen una gran cantidad de herramientas para graficar ecuaciones polares como por ejemplo fooplot, siempre es bueno saber como funcionan y ser capaces de desarrollarlas nosotros mismos. Vamos a hacer un programa en MATLAB que nos permita graficar ecuaciones polares.
Empecemos usando la consola de Octave UPM para ir realizando algunos ejemplos que nos ayudarán a desarrollar nuestro programa. 

Debemos crear lo que sería nuestra tabla de valores. Lo haremos usando vectores y con la función linspace, esta función crea un vector con un número de elementos determinados por nosotros, cuya distancia es igual para todos.
Ejemplo:
linspace(inicio del intervalo, fin del intervalo, cantidad de elementos del vector);
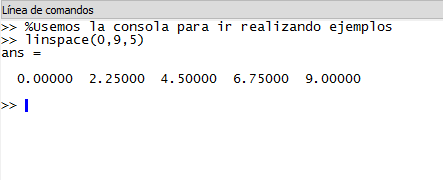
linspace(0,9,5);
0 y 9 sería el intervalo en que se encuentran los 5 elementos del vector que hemos creado, es decir el intervalo [0,9]. 5 obviamente es la cantidad de elementos. Los elementos de nuestro vector serían: [0, 2.25, 4.5, 6.75, 9]

Para graficar en coordenadas polares sabemos que theta (θ) toma valores entre 0 y 2π, entonces este sería el intervalo que usaríamos en la función linspace, nos faltaría saber cuantos elementos tendría nuestro vector. Es importante saber que mientras mayor sea la cantidad de elementos en el vector, será mejor, puesto que estos elementos serán puntos en el plano polar que generarán nuestra gráfica. Y mientras mas puntos tengamos nuestra gráfica será más precisa. Yo recomiendo usar 100 elementos en el vector.
Vamos a crear los valores para θ, yo usaré la variable T como θ para no complicarnos tanto. Esto sería:
t = linspace(0,2*pi,100);
Lo siguiente sería pedir al usuario que ingrese la ecuación polar, es importante mostrar un mensaje diciendo que theta (θ) está representado con la variable t para no presentar confusiones. Sí el usuario quiere graficar  una rosa  de 4 pétalos determinada por cos(2θ) deberá ingresar cos(2*t). 
r = input("Ingrese la ecuación polar. Theta está representada por la variable t");
Finalmente para graficar usaremos la función polar(t,r);
Sí hemos hecho todo bien, para la rosa de 4 pétalos anteriormente mencionada este sería el resultado:

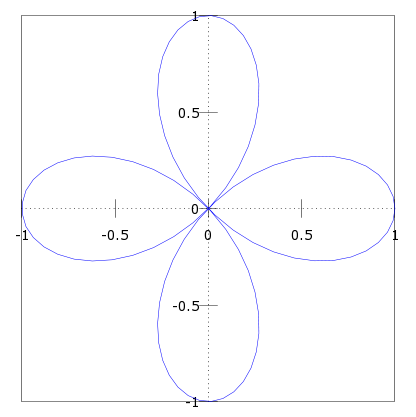
Haciendo nuestro programa para graficar:

% Graficar ecuaciones polares
disp("Bienvenido al graficador de ecuaciones polares\n");
t = linspace(0,2*pi,100);
r = input("Ingrese la ecuacion polar a graficar. Para theta por favor usar la variable t. Ejemplo: cos(theta) = cos(t)\n");
disp("Esta es la grafica de su ecuacion polar\n");
polar(t,r);

Así como fue mencionado antes, creamos un vector de 100 elementos que están entre [0,2π] pedimos al usuario que ingrese la ecuación polar a graficar (utilizando a t como la variable theta). Finalmente se muestra la gráfica. 
El programa en ejecución:

En esta ejecución ingresamos la ecuación de una rosa de 4 pétalos cos(2*t). Pero, ¿si queremos graficar un limazon con rizo? 
La ejecución y la gráfica del limazon con rizo sería:


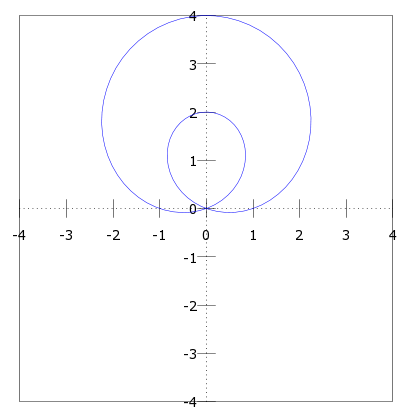
Y ¿sí queremos graficar dos ecuaciones simultáneamente? debemos modificar nuestro código agregando la función hold on. Esta función nos permitirá graficar una nueva ecuación polar sin remplazar la antes graficada. Además de agregar la función hold on agregaremos otras líneas pidiendo una segunda ecuación polar al usuario. Cuando usemos la función polar(t,r); agregaremos otro parámetro para definir el color de las líneas de cada ecuación, esto con el fin de distinguir entre ambas gráficas. Los colores están determinados en su mayoría por  la inicial de su nombre en ingles, ejemplo azul sería b (blue) verde sería g (green). Para graficar una ecuación con lineas azules entonces sería polar(t,r,'b');.

% Graficar dos ecuaciones polares
disp("Bienvenido al graficador de ecuaciones polares\n");
t = linspace(0,2*pi,100);
r = input("Ingrese la primera ecuacion polar a graficar. Para theta por favor usar la variable t. Ejemplo: cos(theta) = cos(t)\n");
disp("Esta es la grafica de su ecuacion polar\n");
polar(t,r,'b');
hold on;
r2 = input("Ingrese la segunda ecuacion polar a graficar. Para theta por favor usar la variable t. Ejemplo: cos(theta) = cos(t)\n");
disp("Esta es la grafica de su ecuacion polar\n");
polar(t,r2,'g');

La ejecución sería:

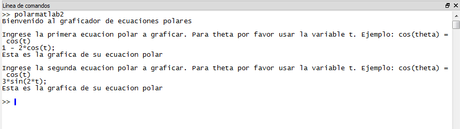
Y nuestra gráfica sería la siguiente: