Muchas áreas de carácter científico-técnico la adecuada elección del software y/o lenguaje de programación empleado es determinante, de cara a la potencia, versatilidad, facilidad de uso y acceso por parte de todos los usuarios en sus propios dispositivos, de manera generalizada y gratuita.
Dentro del software libre, uno de los que últimamente ha tenido una mejora sustancial, con la inclusión de potentes y versátiles nuevos módulos de cálculo simbólico (SymPy), numérico (NumPy, SciPy) y gráfico (PyPlot y Matplotlib) ha sido sin duda Python, y de ahí su vertiginosa evolución y expansión a nivel mundial, no sólo en el ámbito académico, sino también en el científico e industrial. De hecho, basta con echar un vistazo a las numerosas propuestas, tanto de comunidades de desarrolladores como de empresas privadas, surgidas a raíz de la versión de base inicial de Python, como por ejemplo IPython (interface interactivo de fácil uso, que gracias a Jupyter Notebook permite una versión HTML similar a los notebooks de Mathematica o Mapple) o Spyder (entorno integrado para cálculo científico parecido al de Matlab u Octave).
Por otro lado existen versiones completas de desarrollo, integrando Python como soporte de cálculo, pero con editores avanzados de texto para la programación y la depuración de código, ventanas de gráficos y datos, etc. La mayoría de estas plataformas integradas están disponibles para los distintos sistemas operativos Linux, MacOS X y Windows. Entre ellas cabría destacar Enthought Python Distribution (EPD), PyCharm y Anaconda CE (de Continuum Analytics).
Aunque no podamos abarcar todos los aspectos "básicos" del python científico, intentaremos en este resumen dar una idea de las principales librerías un funciones que podemos usar para NILM (Non-Intrusive Load Monitoring) sin olvidar los fundamentos de :Matplotlib y Numpy
Matplotlib: visualización con Python
Nos permite crear :
- Desarrollando gráficos de calidad de publicación con solo unas pocas líneas de código
- Utilizando figuras interactivas que puedan hacer zoom, desplazarse, actualizar ...
Personalizar
- Tomando el control total de los estilos de línea, las propiedades de la fuente, las propiedades de los ejes ...
- Exportando e incrustando en varios formatos de archivo y entornos interactivos
Ampliar
- Explorando la funcionalidad personalizada proporcionada por paquetes de terceros
- Obteniendo más información sobre Matplotlib a través de los numerosos recursos de aprendizaje externos
Matplotlib es en resumen la librería de python para dibujar (equivalente al plot en matlab).
Puede encontrar mas información en el sitio oficial https://matplotlib.org/
Numpy
NumPy es una biblioteca para el lenguaje de programación Python que da soporte para crear vectores y matrices grandes multidimensionales, junto con una gran colección de funciones matemáticas de alto nivel para operar con ellas.
Numpy es pues una librería especializada para operaciones con matrices y vectores
Puede encontrar mas información en l sitio oficial https://numpy.org/

Primeros pasos
Primero, es necesario importarlas al workspace
import numpy as np
import matplotlib.pyplot as plt
Opciones de visualizacion de matplotlib para este notebook
%matplotlib inline
plt.rcParams['figure.figsize'] = (13, 6)
plt.style.use('ggplot')
Otras importaciones
import warnings
warnings.filterwarnings('ignore')
Crear arrays en python es muy sencillo y se puede hacer de forma nativa usando un tipo list. Sin embargo, aquí consideramos arrays del tipo numpy pues esto arrays incluyen funciones que facilitan las operaciones matemáticas y su manipulación
v=[1,2,3] # tipo list
v=np.array([1,2,3]) # array numpy
print (v)
print ("Dimensiones: " + str(v.ndim)) # numero de dimensiones
print ("Elementos: " + str(v.size)) # numero de elementos
print ("Longitud de las dimensiones: " + str(v.shape)) # longitud de cada dimensión
[1 2 3] Dimensiones: 1 Elementos: 3 Longitud de las dimensiones: (3,)
Crear una matriz de 2 x 3:
v=np.array([[1,2,3],
[4,5,6]])
print (v)
print ('Dimensiones: ' + str(v.ndim)) # numero de dimensiones
print ('Elementos: '+str(v.size)) # numero de elementos
print ('Longitud de las dimensiones: '+str(v.shape)) # longitud de cada dimensión
[[1 2 3] [4 5 6]] Dimensiones: 2 Elementos: 6 Longitud de las dimensiones: (2, 3)
Crear una Matriz triple de 2 x 3 x 2 :
v=np.array([[[1,2],
[3,4]],
[[5,6],
[7,8]]])
print (v)
print ("Dimensiones: " + str(v.ndim)) # numero de dimensiones
print ("Elementos: "+str(v.size)) # numero de elementos
print ("Longitud de las dimensiones: "+str(v.shape) )# longitud de cada dimensión
[[[1 2] [3 4]] [[5 6] [7 8]]] Dimensiones: 3 Elementos: 8 Longitud de las dimensiones: (2, 2, 2)
Utilizamos la función reshape para redimensionar los arrays
1 dimension
print (v.reshape(8,))
[1 2 3 4 5 6 7 8]
2 dimensiones
print (v.reshape(2,4))
[[1 2 3 4] [5 6 7 8]]
Matriz Identidad
print (np.identity(5))
[[1. 0. 0. 0. 0.] [0. 1. 0. 0. 0.] [0. 0. 1. 0. 0.] [0. 0. 0. 1. 0.] [0. 0. 0. 0. 1.]]
De unos
print ( np.ones([5,5]))
[[1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.]]
De ceros:
print (np.zeros([5,5]))
[[0. 0. 0. 0. 0.] [0. 0. 0. 0. 0.] [0. 0. 0. 0. 0.] [0. 0. 0. 0. 0.] [0. 0. 0. 0. 0.]]
Las operaciones por definición son elementwise
a=np.arange(5)
b=10*np.ones(5)
print ("vector a: "+str(a))
print ("vector b: "+str(b))
print ("suma b+a: "+str(b-a))
print ("resta b-a: "+str(b+a))
print ("producto b*a: "+str(b*a))
vector a: [0 1 2 3 4] vector b: [10. 10. 10. 10. 10.] suma b+a: [10. 9. 8. 7. 6.] resta b-a: [10. 11. 12. 13. 14.] producto b*a: [ 0. 10. 20. 30. 40.]
El producto de los vectores es:
a.dot(b)
100.0
Para las matrices tenemos que:
a=np.identity(3)
b=np.array([[1,2,3],[4,5,6],[7,8,9]])
print ("matriz a:\n"+str(a))
print ("matriz b:\n"+str(b))
print ("producto a*b:\n"+str(a.dot(b)))
print ("producto elementwise a.*b:\n"+str(a*b))
matriz a: [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]] matriz b: [[1 2 3] [4 5 6] [7 8 9]] producto a*b: [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]] producto elementwise a.*b: [[1. 0. 0.] [0. 5. 0.] [0. 0. 9.]]
Vector formado por un rango de valores:
print ("De 0 a 10: " + str(np.arange(10)))
print ("De 10 a 20 de paso 0.5: "+str(np.arange(10,20,0.5)))
De 0 a 10: [0 1 2 3 4 5 6 7 8 9] De 10 a 20 de paso 0.5: [10. 10.5 11. 11.5 12. 12.5 13. 13.5 14. 14.5 15. 15.5 16. 16.5 17. 17.5 18. 18.5 19. 19.5]
Función linspace:
np.linspace(0,2*np.pi,10) # de 0 a 2*pi en 10 puntos equidistantes
array([0. , 0.6981317 , 1.3962634 , 2.0943951 , 2.7925268 ,
3.4906585 , 4.1887902 , 4.88692191, 5.58505361, 6.28318531])
función random:
np.random.rand(10)
array([0.63623588, 0.83924558, 0.35833155, 0.33835148, 0.53247758,
0.0950348 , 0.2805706 , 0.47285484, 0.8696919 , 0.78361161])
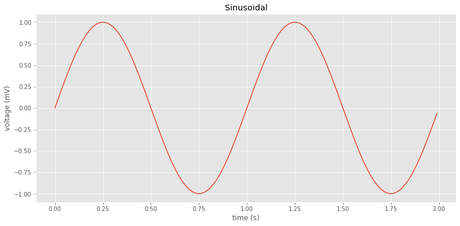
Dibujar una función seno
t = np.arange(0.0, 2.0, 0.01)
s = np.sin(2*np.pi*t)
plt.plot(t, s)
plt.xlabel('time (s)')
plt.ylabel('voltage (mV)')
plt.title('Sinusoidal')
plt.grid(True)
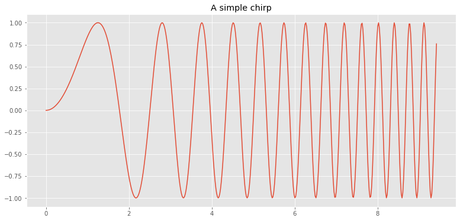
Dibujar una función chirp
x=np.linspace(0,3*np.pi,500)
plt.plot(x,np.sin(x**2))
plt.title("A simple chirp")
Text(0.5, 1.0, 'A simple chirp')
Definir una función en Python
En python, las funciones pueden estar definidas en cualquier parte pero siempre antes de su llamada. En python, las anidaciones (bucles, if conditions, functions, etc.) se realizan mediante indentación, no existe el statement end. Las funciones se definen así:
def funcion_suma(x):
suma=0
for i in x:
suma=suma+i
return suma
v=np.arange(10)
print (funcion_suma(v))
45
Aunque, como hemos dicho antes, numpy facilita las operaciones matemáticas y ya incluye una serie de operaciones:
print (v.sum())
print (v.cumsum())
print (v.mean())
45 [ 0 1 3 6 10 15 21 28 36 45] 4.5
Para saber más sobre numpy:
https://docs.scipy.org/doc/numpy-dev/user/quickstart.html http://www.sam.math.ethz.ch/~raoulb/teaching/PythonTutorial/intro_numpy.html(O simplemente "googleando": numpy tutorial)
Pandas
Pandas (Python Data Analysis Library) es una librería de python para el análisis y manipulación de una gran cantidad de datos. También facilita el uso de "timeseries"
La llamada a la librería es:
import pandas as pd
Dado un archivo csv, la función read_csv carga los datos en un dataframe
# El parámetro parse_dates indica a pandas que al cargar este csv la primera columna [0] es de tipo datetime
df=pd.read_csv('data/events.csv',parse_dates=[0])
Las primeras N filas del dataFrame se puede visualizar de la siguiente forma
N=4
df.head(N)
Y las N últimas columnas
df.tail(N)
Podemos filtar por un cierto valor
df[df.phase=='B'].head()
Y hacer agrupaciones
df2=df.sort_values(['label','phase']).groupby(['label','phase']).count()
df2
161 rows × 1 columns
Las nuevas columnas se crean fácilmente. Compatible con numpy.
df['x']=25*np.random.rand(len(df))
df['y']=100*np.sin(2*np.pi*np.linspace(0,2*np.pi,len(df)))
df['z']=df.x+df.y
df.head(5)
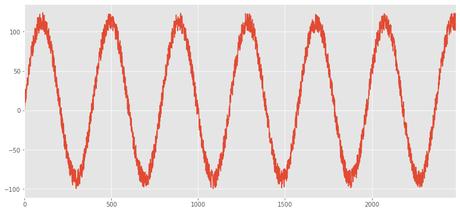
Para dibujar sólo necesitamos usar la función plot
df.z.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7f6e3ba88080>
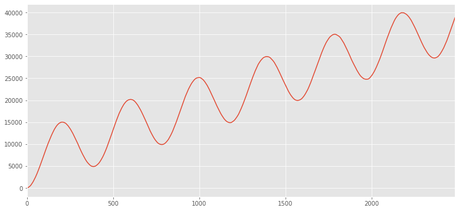
Existen ciertas funciones predefinidas que facilitan los cálculos
df.z.cumsum().plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7f6e3b801e80>
Y se pueden concatenar
# Si integramos y derivamos obtenemos la misma señal
df.z.cumsum().diff().plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7f6e32625320>
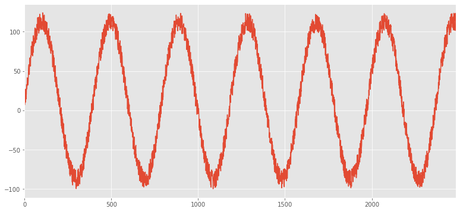
Unas de las herramientas más potentes de pandas es la manipulación de timeseries
df.index=df.timestamp
df.z.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7f6e325e6518>
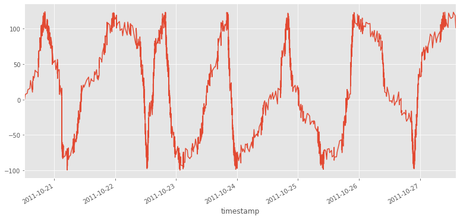
Podemos filtar por fechas
d1='2011-10-21'
d2='2011-10-23'
df[(df.index>d1)&(df.index<d2)].z.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7f6e325d5588>
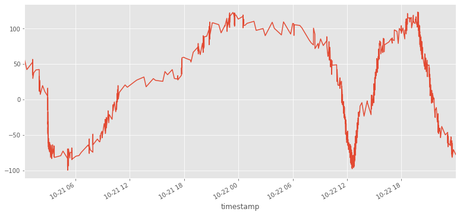
Existe una gran flexibilidad a la hora de resamplear un dataframe
# Cada día
df.resample('1D',how='sum')
# Cada 6 horas
df.resample('6H',how='count')
Para aprender más sobre pandas:
http://pandas.pydata.org/pandas-docs/stable/tutorials.html http://pandas.pydata.org/pandas-docs/stable/10min.htmlVamos a crear un detector de eventos.
Dado el consumo eléctrico de una vivienda (voltage y corriente) queremos detectar en que momento se produce una conexión de un dispositivo. Para ello, filtraremos la señal sinusoidal obteniendo el valor eficaz de la corriente cada cierto intervalo. Los cambios en el valor eficaz van a determinar las conexiones y desconexiones de los distintos dispositivos. Derivando este valor eficaz, obtenemos picos en los que existe un cambio en el valor eficaz y, por lo tanto, posibles candidatos a eventos de conexión/desconexión. Finalmente, usando un detector de picos filtraremos los eventos reales del resto.
Mediremos nuestros resultados usando métricas estándar de NILM.
Paso por paso
Importar pandas, numpy y matplotlib tal y como se ha visto anteriormente
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
Definir una funcion llamada rms_function que devuelva un valor rms y que tenga como parámetro de entrada un vector de valores
# función rms
def rms_function(x):
return np.sqrt(np.mean(np.square(x)))
Usar el siguiente path para cargar los datos en un dataframe df de pandas. Como parámetros: el índice es la columna 0 ( index_col) y la fecha está en la columna 1 ( parse_dates)
path='data/smart_meter_data.csv'
df= ...
path='data/smart_meter_data.csv'
df=pd.read_csv(path, parse_dates=[1],index_col=[0])
Mostrar las 5 primeras columnas del dataframe
df.head(5)
Imprimir mínimo y máximo de datetime y la diferencia de ambos
print (df.datetime.min())
print (df.datetime.max())
print (df.datetime.max()-df.datetime.min())
2011-10-20 12:21:58.973000 2011-10-20 12:23:03.713996 0 days 00:01:04.740996
Seleccionar datetime como índice del dataframe df
df.index=df.datetime
Periodo y frequencia de muestreo
# frecuencia
ts=df.datetime.diff().mean().total_seconds()
print (str(ts)+' seconds')
fs=1/ts
print ( str(fs)+' Hz')
8.3e-05 seconds 12048.192771084337 Hz
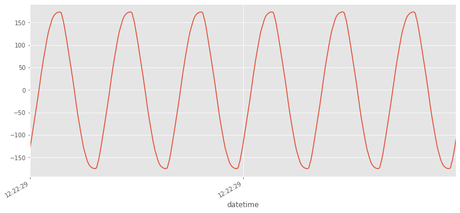
Dibujar Voltage (v) haciendo zoom en el intervalo de 100ms (6 periodos aproximadamente)
d1='2011-10-20 12:22:29.9'
d2='2011-10-20 12:22:30'
df[(df.index>d1)&(df.index<d2)].v.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7f6e2b9f86d8>
df.i.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7f6e2e274d30>
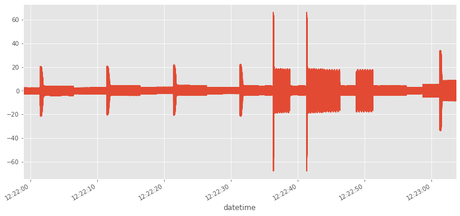
Resamplear mediante la función resample de pandas a 50ms ('50L'). La función rms_function se pasará como parámetro para obtener cada valor del resampleado. El resultado debe de guardarse en un dataframe nuevo llamado rms . Dibujar el resultado.
rms=pd.DataFrame(df.i.resample(....))
rms=pd.DataFrame(df.i.resample('50L',how=rms_function))
rms.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7f6e2f8848d0>
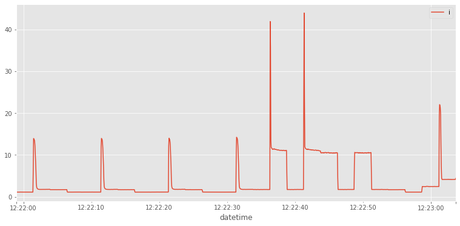
Hacer la derivada del dataframe rms y guardar el resultado en rms_diff.
rms_diff=rms.diff()
Dibujar el resultado (rms_diff)
rms_diff.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7f6e2f7f9fd0>
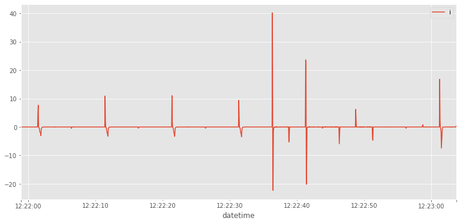
Guardar los valores de la columna "i" en una variable "y" en forma de array
y=rms_diff.i.values
Modifica los parámetros th_noise y dist de la función detect_peaks para obener los índices de los eventos y evaluar las métricas. Realizar el proceso 3 veces. ¿ Con qué valores de th_noise y dist se obtienen mejores resultados en las métricas?
th_noise=5
dist=5
from detect_peaks import detect_peaks
indexes=detect_peaks(y,mph=th_noise,mpd=dist)
dates=rms_diff.ix[indexes].index
Cuantos eventos hemos detectado
print (str(len(indexes))+' eventos detectados')
8 eventos detectados
Dibujamos los eventos y la corriente en una misma gráfica
plt.vlines(dates,-80,80)
df.i.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7f6e2f79ca58>
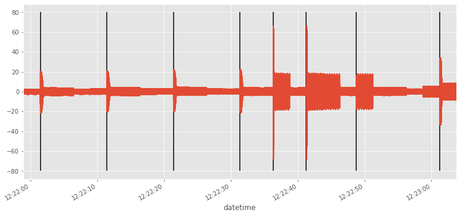
Métricas
from IPython.display import Image
Image(filename='metricas1.png')

Image(filename='metricas2.png')

Obtener las métricas: recall, precision y F1
FP=0.
P=9.
N=len(df)-P
TN=N-FP
P=9.
N=len(df)-P
TP=8.
FP=0.
FN=1.
TN=N-FP
recall=TP/(TP+FN)
precision=TP/(TP+FP)
F1=2*precision*recall/(precision+recall)
print (recall)
print (precision)
print (F1)
0.8888888888888888 1.0 0.9411764705882353
* Parámetros optimizados: * th_noise=0.1 y dist=5
* Con esto obtenemos : * recall=1, precision=1 y F1=1;

