La falsa curva de Fibonacci

Para los que no somos matemáticos, nuestros conocimientos sobre Fibonacci se basan en su famosa secuencia (1, 1, 2, 3, 5, 8, 13, 21, etc), la espiral áurea o el número áureo (fi, φ, o tau, Τ). Un conjunto de conceptos que parecen repetirse constantemente en la naturaleza hasta hacernos pensar que cualquier espiral es susceptible de repetir el mismo patrón. Incluso podríamos creer que todo sigue la secuencia, como si fuera una clase de orden superior, divino.
En base a esto, es fácil mostrar como estos patrones se muestran en la naturaleza, sin intervención humana. El ejemplo más clásico es la concha de nautilus. Pues bien, observar la imagen superior. Si no os fiáis de mí es algo que podéis hacer vosotros mismos. En teoría, según la imagen que se suele mostrar, la espiral áurea coincide con el borde exterior de la concha hasta llegar, siguiendo su contorno, hasta el centro. Yo, y tú puedes repetirlo, he superpuesto la espiral e incluso he procurado que empiece y termine en los mismos puntos que la espiral de la concha. A pesar de eso, no coinciden. ¿Podría ser que no todas las espirales del mundo se corresponden con la espiral áurea? Efectivamente. Aún así, la espiral áurea aparece en la estructuras de muchas plantas, que no todas. Ni siquiera en todas las que siguen un patrón espiral. La filotaxis, es decir, la disposición de las hojas en la planta, muestra que la posición de las hojas va más allá de la espiral. Vi Hart lo explica muy bien en sus tres vídeos (aquí el primero de ellos). Lo dicho de las plantas se puede aplicar a galaxias espirales, remolinos, huracanes, caracoles, entre otros.
Como se habla de ella como si fuera omnipresente, los ejemplos que se dan son muy variados. Una supuesta muestra son los ocelos de la cola del pavo real, los cuales se dicen que forman la espiral áurea, aunque dependiendo de la posición de la cola, podría ser cualquier otra. El problema en estos y otros ejemplos es que sus espirales se parecen mucho. Como explica Vi Hart en el comienzo del primer vídeo, hay varios tipos de espirales: pueden mantener siempre la misma distancia en cada revolución, aumentarla progresivamente o disminuirla. La espiral áurea, como otras muchas, se encuentra en el segundo tipo. A simple vista, y con algunos datos falsos, cualquier espiral puede ser considerada una espiral áurea. El girasol se muestra casi tanto como la imagen del nautilus. Yo he intentado repetir la misma prueba. He procurado que la espiral áurea encaje en una de las espirales del girasol, y aún así no ha funcionado. Si lo repetís, e incluso si giráis la imagen, el resultado será el mismo. Habrá algún girasol en el que coincida o en el que se parezca, pero si no es una regla mágica que se cumpla siempre, pierde su magia. Las piñas también cumplen esta norma. Aunque puedes encontrar muchas donde el número de espirales corresponda al número de Fibonacci (5 u 8, por ejemplo), también puedes ver otras que no cumplan esta regla. Sería el equivalente con piñas a encontrar un trébol de cuatro hojas.
Por otra parte, se suele decir que las matemáticas explican esta distribución, pero más bien describen los patrones que permiten a la biología, física, o disciplina que corresponda, explicar la razón de esa posición
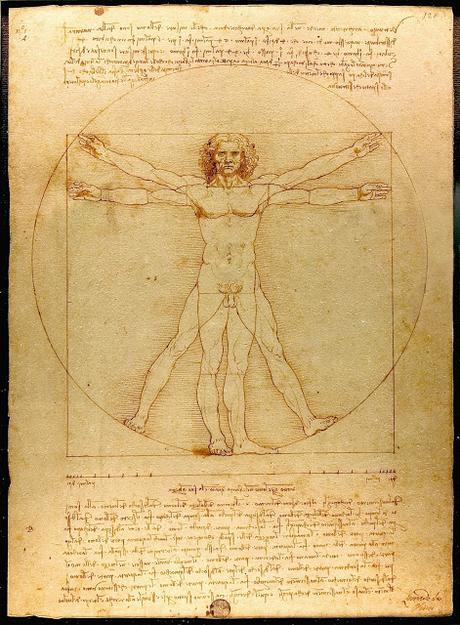
Aparte de esto, como cualquier cosa que tocan los "expertos", se producen multitud de malinterpretaciones. La supuesta proporción de belleza dice que en las personas bellas, la división de la altura de la persona y la distancia del ombligo al suelo coincide con el número áureo. Esta afirmación ni siquiera se cumple en el hombre de Vitruvio, a pesar de que hay quienes aseguran erróneamente que Leonardo da Vinci acuñó estas proporciones perfectas (quien solo necesitaba cambiar un poco la altura del ombligo para que los cálculos encajaran).

Gardenia con 6 pétalos

También se dice que los rectángulos áureos son los más bellos, como si la belleza dejara de ser subjetiva para ver un cuadrilátero. Pero las afirmaciones absurdas no se quedan ahí, como la que dice que la letra griega phi proviene de Fidias, arquitecto del Partenón. Los creacionistas por su parte buscan confirmar sus convicciones a través de muestras sesgadas en la naturaleza, como las flores cuyos pétalos coinciden con los números de la secuencia de Fibonacci. No solo ignoran a aquellas flores con un número de pétalos distintos, sino también a las que no tienen. 

Algunos cuadrados se han convertido en rectángulos para que  todo coincida

La lista de bobadas es interminable. Muchas veces se escogen los datos justos para apoyar conclusiones falsas, ignorando los datos que no convienen, o se dan conclusiones en las que, si comprobamos los datos, no proporcionan el mismo resultado. Respecto a las plantas y otros elementos, la conclusión a la que se puede llegar es que muchas se disponen en espiral, sin que tenga que ser la de Fibonacci.
Fuente: Lock Haven University