Las matemáticas de la homeopatía

¿Alguno de mis lectores sabe de homeopatía? Bueno, yo no sé demasiado, pero sí que sé dónde aprender Qué es la Homeopatía de una forma racional.
La web que os he enlazado es una idea original de Rinze, autor de Las Penas del Agente Smith y FerFrias, autor de El Fondo del Asunto pero que se ha convertido en un proyecto común de los colaboradores y autores de Amazings.
Tan sólo os quiero rescatar una parte de la información que se puede encontrar allí sobre la homeopatía que está muy relacionada con las matemáticas.

La homeopatía clásica se define habitualmente como el sistema médico basado en el uso de cantidades diminutas (inifinitesimales) de sustancias que en grandes dosis producirían síntomas parecidos a los de la enfermedad que está siendo tratada.

y su origen se remonta al médico alemán Christian Friedrich Samuel Hahnemann. Según su procedimiento, la forma de preparar una dilución homeopática consistía en añadir a 1 ml de sustancia original, 99 ml de agua. Esto se conoce como 1 centesimal de Hahnemann (CH) y corresponde, si las matemáticas no me fallan, con una solución al 1%, es decir, .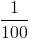
Una dilución homeopática de 2CH se conseguiría añadiendo 1 ml de la dilución 1CH con 99 ml de agua. Matemáticamente, tendremos una solución de 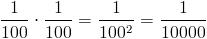, es decir del 0'01%. Y así sucesivamente.
Cualquier matemático se dará cuenta que, por un proceso inductivo, una dilución de 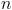CH correspondería con una solución de 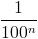, es decir, 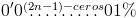. Y claro todo el mundo (matemático) sabe que la sucesión 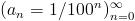tiende muy rápido a 0. Así que, por ejemplo un medicamento con una dilución de 12CH (que por lo visto es algo medio, es decir, ni mucho ni poco, en homeopatía) contiene una solución al 0,000000000001% o lo que es lo mismo, hay 1 molécula de principio activo por cada 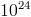, es decir 1 entre 1 cuatrillón.
En fin, yo sólo sé un poco de Matemáticas y a ellas me remito para darme cuenta que esto de la homeopatía no parece que sea de por sí muy efectiva.
De todas formas, os remito a la web Qué es la Homeopatía y a los enlaces que en ella podréis encontrar, para que vosotros mismos os creéis (de crear) vuestra propia opinión, que es lo que nos hace seres racionales.
Tito Eliatron Dixit
PD: No soy muy amigo de participar en iniciativas de este tipo sobre las que, habitualmente, no sé más que la mayoría. Pero este es un caso especial por razones muy personales. Y porque con la lectura de la web referenciada y sus matemáticas, he aprendido y me he creado mi propia opinión.