Las Matemáticas Detrás De La Música

Antes de comenzar, puedes echar un vistazo a mi artículo “¿existen sólo 12 notas musicales?”, para que te des una idea de que hablaré aquí.

Después de leerlo te podrás tener una noción de cómo las matemáticas están involucradas en la división de las octavas musicales, y como esto engaña a nuestros oídos y los hace creer que un La3 suena igual a un La4.

En un resumen simple, la distancia entre las frecuencias de cada octava (ya sea de La0 a La7 o de Do#1 a Do#7) es una progresión geométrica. Si se grafica esto, veremos una curva exponencial.

Bien, pues en sí toda la progresión de las notas sigue este mismo patrón.

Si alguna vez te preguntaste en el curso de matemáticas: ¿para qué me va a servir esto? Quizá ahora te respondas a ti mismo que para todo. O si no seguiste por la rama de ingeniería, podrás decir que al final no te sirvió para nada. Pero la realidad es que las matemáticas están metidas hasta en la sopa, y aunque tú no las apliques, todo lo que usas, miras y sabes, claro que lo hace. Hasta la música.

Si tomamos como nota de referencia, por ejemplo Do1, veremos que la frecuencia que tiene esta nota es de 32.7 Hz. La nota que le sigue (recordemos que son 12 notas musicales), es Do#1. Esta nota tiene una frecuencia de 34.65 Hz. La que sigue, Re1, tiene frecuencia de  36.71 Hz.

Paremos aquí.

Si calculamos la diferencia entre las frecuencias, nos daremos cuenta que de Do1 a Do#1 ésta es de 1.95 Hz, mientras que de Do#1 a Re1 es de 2.06 Hz. La diferencia no es lineal, es decir, no se le suma la misma cantidad de Hertz cada vez.

Es por esto que si queremos calcular la progresión, no bastará con sumar números de esta forma:

F = x + a + b + c + …

Porque si “F” es la frecuencia buscada y “x” es la frecuencia de la nota inicial, tendríamos que sumar cada vez un número diferente, y esa forma no es práctica.

Así pues, si la progresión es geométrica, habrá que encontrar la razón a la cual esta frecuencia aumenta.

Para ello podemos suponer que:

F = x(z)

Dónde “F” es la frecuencia que buscamos, “x” es la frecuencia de la que partimos y “z” es esa razón a la que cambia la frecuencia.

Está claro que con cada nueva nota aumentada, la frecuencia aumentará a esa misma razón, dado que así está ya establecida la escala musical. Así pues, habrá que multiplicar tantas veces nuestra frecuencia inicial por la razón dada.

Si queremos encontrar, por ejemplo, la frecuencia 8 semitonos más allá de Do1, la cosa sería algo así:

F = Do1 (z)(z)(z)(z)(z)(z)(z)(z)

Y sí recordamos un poco de las clases de matemáticas, esto es igual a:

F = Do1 z8

Ahora solo es necesario reemplazar valores. La frecuencia de Do1 ya habíamos dicho, es 32.7 Hz. 8 Semitonos más allá, encontramos a Sol#1, cuya frecuencia es de 51.9 Hz.

Así:

51.9 Hz = 32.7 Hz (z)8

Con un simple despeje matemático podemos encontrar que “z” vale 1.05944265.

Esta es la razón a la que aumenta cada semitono.

51.9 Hz = 32.7 Hz (1.05944265)8

Ya habíamos dicho que es un incremento exponencial, así que para dejarlo en estos términos solo hay que tratar un poco los números y obtendremos esto:

F = x e0.0578z

En esta ocasión F es la frecuencia que buscamos, “x” es de la que partimos y “z” es cuántos semitonos hay de diferencia entre una y otra.

Ya por el artículo mencionado al principio sabemos que cada octava tiene el doble del valor de la frecuencia de la anterior. Y sabemos que la más fácil de analizar es la nota La, ya que sus números son cerrados.

Así tomemos a la mágica La4 cuya frecuencia es 440 Hz. Usemos la ecuación para encontrar el valor de La5, que ya sabemos que es el doble, o sea 880 Hz. Pero solo comprobemos la ecuación.

Agarremos una calculadora y metamos esos datos. Recordemos que entre cada octava hay una distancia de 12 semitonos, así que le valor de “z” que usaremos será 12.

La5 = 440 Hz e0.0578(12)

La5 = 880.3985 Hz.

No obtuvimos los 880 Hz cerrados. Qué problema.

O tal vez no. En realidad fue porque ese número, 0.0578, tiene muchos más decimales. Probemos usando al menos 16, que sería:

0.0577647896688925

Ahora sí. Repitamos la operación y obtendremos un valor de:

La5 = 880.027 Hz.

Más cerca.

Y esto se puede hacer con cualquier nota musical.

Hoy día existe la magia del internet y podemos buscar a que frecuencia debe estar cada nota, y así todo resulta muy sencillo a la hora de afinar nuestros instrumentos. Pero solo es una muestra de cómo las matemáticas están detrás de todo.

Finalmente, dejo una gráfica de la progresión de las primeras dos octavas, que van desde Do1 hasta Si2, marcando a Do1 como la nota 0 y a Si2 como la nota 23. Dónde se puede apreciar claramente la progresión con forma exponencial.

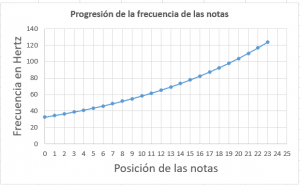
De nueva cuenta, salta la pregunta: ¿por qué esta progresión logarítmica suena tan bien a nuestros oídos? ¿Habrá otro tipo de progresión que suene agradable?

Bien, pues la primera es cuestión de fisiología humana, o quizá es porque ya nos acostumbramos. Aun así, no deja de ser sorprendente. La segunda pregunta, se podría contestar intentando afinar nuestro instrumento con una progresión diferente. Quizá una parabólica, o polinómica. Quién sabe.