Tanto si te dedicas a la ciencia de datos, como si no, es importante conocer qué algoritmos se utilizan a la hora de crear esos clusters que van a permitir a la empresa, poder agrupar a sus clientes para lograr comunicarse con ellos de manera más personalizada.
Pero antes, es necesario que sepas que clustering o análisis de grupos o agrupamiento, consiste en reunir objetos o personas por similitud, en grupos o conjuntos de manera que los miembros que lo componen tengan características comunes entre sí y los grupos sean lo más diferenciados.
Para hacerlo, se utilizan lo que se llama, algoritmos de agrupamiento. Estos, son un procedimiento de agrupación de una serie de vectores de acuerdo con un criterio, que por lo general son la distancia y la similitud.
En Data Science, se utiliza el análisis de agrupamiento para obtener información valiosa de nuestros datos, y ver en qué grupos caen los puntos de datos cuando aplicamos un algoritmo de agrupamiento.
Vamos a ver los algoritmos más populares, así como sus ventajas y sus desventajas. Vamos a ello.
#1. K-Means Clustering
Puede que este sea el algoritmo de agrupación más conocido, ya que es el que primero se enseña en las clases de introducción a la ciencia de datos y en machine learning, además, es muy fácil de implementar.
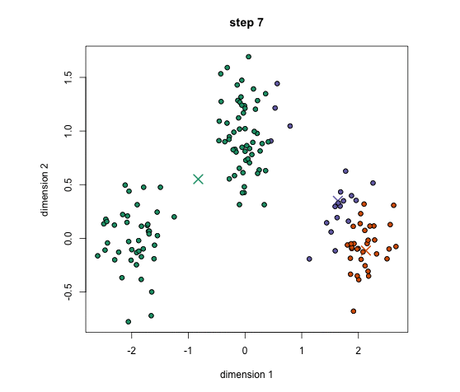
K-means tiene la ventaja de que es bastante rápido, ya que se realizan muy pocos cálculos. Sin embargo, tiene un par de desventajas.
La primera de ellas es, que debes seleccionar cuántos grupos/clases hay. Esto no siempre es trivial e, idealmente, con un algoritmo de agrupamiento, nos gustaría que este los descifrara por nosotros. Otra desventaja podría ser que, K-means comienza con una elección aleatoria de centros de conglomerados y, por lo tanto, puede generar diferentes resultados de conglomerados en diferentes ejecuciones del algoritmo. Por lo tanto, los resultados pueden no ser repetibles y carecer de consistencia. Otros métodos de clusterización son más consistentes.
#2. K-Nearest Neighbours
El algoritmo de k-nearest neighbours, también conocido como KNN o k-NN, es un clasificador de aprendizaje supervisado no paramétrico, que utiliza la proximidad para hacer clasificaciones o predicciones sobre la agrupación de un punto de datos individual. Aunque puede utilizarse tanto para problemas de regresión como de clasificación, normalmente se utiliza como algoritmo de clasificación, partiendo de la base de que se pueden encontrar puntos similares cerca unos de otros.
La principal desventaja de este algoritmo es el incremento de los tiempos de cálculo a medida que aumenta el número de ejemplos y/o predictores. Actualmente, no es un problema grave dada la mejora de recursos de computación existentes.
#3. Mean-Shift Clustering
Este es un algoritmo basado en una ventana deslizante que intenta encontrar áreas densas de puntos de datos. Es un algoritmo basado en el centroide, lo que significa que el objetivo es ubicar los puntos centrales de cada grupo/clase. Funciona actualizando los candidatos para que los puntos centrales sean la media de los puntos dentro de la ventana deslizante. Estas ventanas candidatas luego se filtran en una etapa de pos-procesamiento para eliminar prácticamente todos los duplicados, formando el conjunto final de puntos centrales y sus grupos correspondientes.
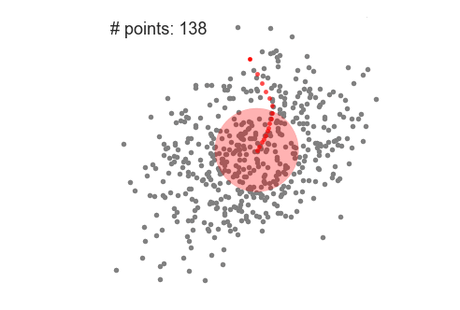
A diferencia del agrupamiento de K-means, no es necesario seleccionar el número de clusters, ya que el desplazamiento de la media lo descubre automáticamente. Esa es una gran ventaja. El hecho de que los centros de los cúmulos converjan hacia los puntos de máxima densidad también es bastante deseable, ya que es bastante intuitivo de entender y encaja bien en un sentido natural basado en datos. El inconveniente es que la selección del tamaño de ventana/radio "r" puede no ser trivial.
#4. Clustering espacial basado en la densidad de aplicaciones con ruido (DBSCAN)
DBSCAN es un algoritmo agrupado basado en la densidad, similar al mean-shift, pero con un par de ventajas notables.
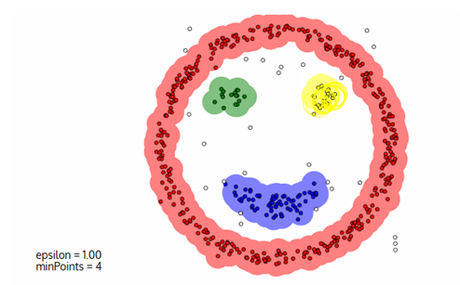
En primer lugar, no requiere una cantidad determinada de clústeres en absoluto. También identifica los valores atípicos como ruidos, a diferencia del cambio de media, que simplemente los arroja a un grupo incluso si el punto de datos es muy diferente. Además, puede encontrar clústeres de tamaño y forma arbitrarios bastante bien.
El principal inconveniente de DBSCAN es que no funciona tan bien como otros cuando los grupos tienen una densidad variable. Esto se debe a que la configuración del umbral de distancia ε y minPoints para identificar los puntos de vecindad variará de un grupo a otro cuando la densidad varía.
#5. EM (Expectation-Maximization) Clustering, usando una mezcla de modelos gausianos.
El algoritmo K-Means es quizás el más utilizado, sin embargo, hay ciertas distribuciones de los datos, sobre los que este algoritmo no es tan eficaz, ya que funciona sobre agrupaciones circulares.
Por ejemplo, en estos casos como el que adjunto, K-Means no puede manejarlo, ya que los valores medios de los grupos están muy juntos. K-Means también falla en los casos en que los clusters no son circulares, nuevamente como resultado de usar la media como centro del cluster.

Estos modelos de mezcla gausiana, nos ofrecen una mayor flexibilidad que los K-means. Con estos, tenemos dos parámetros para describir la forma de los grupos. De esta manera, los grupos pueden tomar cualquier tipo de forma elíptica.
Este tipo de modelos tiene principalmente 2 ventajas: son mucho más flexibles en términos de covarianza de clúster que K-Means; y que, debido al parámetro de desviación estándar, los grupos pueden adoptar cualquier forma de elipse, en lugar de estar restringidos a círculos, como es el caso de los K-means.
#6. Cluster por jerarquías.
Los algoritmos de agrupamiento jerárquico se dividen en 2 categorías: de arriba hacia abajo o de abajo hacia arriba.
Los algoritmos de abajo hacia arriba tratan cada punto de datos como un único grupo desde el principio y luego fusionan (o aglomeran) sucesivamente pares de grupos hasta que todos los grupos se fusionan en un solo grupo que contiene todos los puntos de datos. Por lo tanto, el agrupamiento jerárquico de abajo hacia arriba se denomina agrupamiento aglomerativo jerárquico o HAC (hierarchical agglomerative clustering). Esta jerarquía de conglomerados se representa como un árbol (o dendrograma). La raíz del árbol es el único racimo que reúne todas las muestras, siendo las hojas los racimos con una sola muestra.
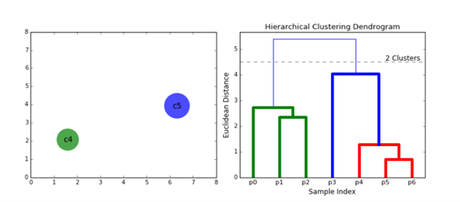
El agrupamiento jerárquico no requiere que especifiquemos el número de clústeres e incluso podemos seleccionar qué número de clústeres se ve mejor ya que estamos construyendo un árbol. Además, el algoritmo no es sensible a la elección de la métrica de distancia; todos tienden a funcionar igual de bien, mientras que con otros algoritmos de agrupamiento, la elección de la métrica de distancia es crítica. Un caso de uso particularmente bueno de los métodos de agrupación en clústeres jerárquicos es cuando los datos subyacentes tienen una estructura jerárquica y desea recuperar la jerarquía; otros algoritmos de agrupamiento no pueden hacer esto. Estas ventajas del agrupamiento jerárquico tienen el costo de una menor eficiencia, ya que tiene una complejidad temporal de O(n³), a diferencia de la complejidad lineal de K-Means y GMM.
Como ves, existen un gran número de algoritmos de agrupación, los cuales funcionarán mejor o peor en base a tus datos o tus objetivos, por poner un ejemplo. Para tener éxito, es necesario disponer del talento dentro de tu compañía, el cual sea capaz de crear la clusterización adecuada a tus necesidades. ¿Te ayudamos?
