los conejos o las abejas de Fibonacci

los conejos o las abejas de Fibonacci

La sucesión
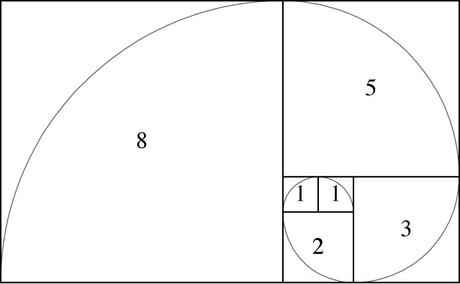
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
es un ordenamiento de números naturales que surge de la suma de los dos términos anteriores. Esto es: 1 + 1 = 2; 2 + 1 = 3; 3 + 5 = 8; etc.
Esta sucesión tiene una propiedad que llama la atención: si dividimos cada término por el anterior y formamos una nueva sucesión, está tiende a estabilizarse en torno a un número que es igual a la semisuma de la raíz cuadrada de 5 más uno, un número irracional, aproximadamente 1,618033… conocida como la proporción áurea.
¿Por qué este número es interesante? Porque nos topamos con él, una y otra vez, cada vez que examinamos la naturaleza. Está relacionado con la disposición de las hojas, pétalos, las espirales de una piña, las proporciones anatómicas de los seres humanos, las espirales del interior de un caracol, etc., etc., etc. No importa adónde vayan, ahí aparece la proporción áurea, por lo que no tardó mucho para que se lo asociara con lo místico.
La sucesión con la que empezamos este post, es una invención de Leonardo de Pisa, un gran matemático italiano del principios del siglo XIII. Podemos decir que esa sucesión es un divertimento en la carrera de Leonardo porque él fue el difusor del sistema de numeración indoarábigo que usamos actualmente a partir de la publicación en 1202 de “El libro del ábaco (o del Cálculo)”.
El papá de Leonardo de Pisa hijo de Guglielmo de la familia Bonacci fue conocido como el hijo de Bonacci, esto es, filius Bonacci, abreviado como Fibonacci. Y ése es el nombre con el que se conoce a la sucesión con la que empezamos el post: la sucesión de Fibonacci.
En “El Libro del Ábaco (o del Cálculo)”, Leonardo afirma que la sucesión surgió al considerar un problema práctico, la cría de conejos. Un hombre tenía una pareja de conejos en un lugar cerrado y deseaba saber cuántos se reproducirían al final del año, teniendo en cuenta que tardan un mes en tener pareja y otro en reproducirse.
El esquema sería:
Principio del mes:
Nace una pareja de conejos.
Parejas en total: 1
Fin del mes 1:
La pareja A tiene un mes de edad. Se cruza la pareja A.
Parejas en total: 1 + 0 = 1
Fin del mes 2:
La pareja A da a luz a la pareja B y se vuelve a cruzar.
Parejas en total: 1 + 1 = 2
Fin del mes 3:
La pareja A da a luz a la pareja C. La B cumple el primes mes y se cruza con la A.
Parejas en total: 2 + 1 = 3
etcétera o como dirían en el barrio… así.
Hasta acá, no hay porque desconfiarle a Leonardo sobre el origen de su sucesión. Pero hay historiadores de la matemática que empezaron a notar cierta artificialidad en el argumento. No es tan claro que la cría de conejos produzca eventos con esa estructura. Por lo que empezaron a sospechar que el fin didáctico que abrigaba a Leonardo estaba reñido con la verdad.
Fue entonces que empezaron a hurgar en la historia de Leonardo cuyo padre, rico comerciante, fue cónsul de Pisa en el norte de África donde tuvo negocios, más específicamente en Bugia (hoy conocida como Bejaia) en Argelia. Siendo niño, Leonardo acompañó a su padre en su función diplomática y mercantil por esas tierras. Justamente, Bejaia era uno de los centros apicultores del Mediterráneo y un importante exportador de cera de abeja. (Recordemos que cierto tipo de vela se conocía en Francia con el nombre de Bougie o Bejaia, el nombre de la ciudad).
Leonardo no sólo se interiorizó de los estudios matemáticos árabes que luego difundió en Occidente sino que tuvo que conocer la industria de la producción de cera de abejas. Y por la apicultura habrá conocido la condición de los machos de las colmenas que tienen un árbol genealógico muy particular. Justamente, el zángano (1), macho de la abeja, no tiene padre pero sí madre (1, 1), dos abuelos (los padres de la reina) (1, 1, 2), tres bisabuelos (el padre de la reina no tiene padre) (1, 1, 2, 3), cinco tatarabuelos (1, 1, 2, 3, 5), ocho trastatarabuelos (1, 1, 2, 3, 5, 8) y así sucesivamente. La estructura es conocida: la sucesión de Fibonacci.
Claro está que hay otras teorías sobre la fuente de inspiración de Leonardo de Pisa para su célebre sucesión. Pero ésta es la que nos resultó más seductora para contarla en este blog.
(¡Gracias Javier!)

FUENTES:
La entrada de The Mac Tutor History of Mathematics Archive de la Universidad de San Andrés en Escocia:
http://www-history.mcs.st-and.ac.uk/Biographies/Fibonacci.html
y el artículo de T. C. Scott y P. Marketos en el mismo sitio:
http://www-history.mcs.st-andrews.ac.uk/Publications/fibonacci.pdf
El artículo en Wikipedia de Leonardo de Pisa:
http://es.wikipedia.org/wiki/Leonardo_de_Pisa
y de la Sucesión de Fibonacci:
http://es.wikipedia.org/wiki/Sucesión_de_Fibonacci