Notas sobre aprendizaje por refuerzo (IX): aprendizaje de políticas y el ascenso de gradiente

En esta ya larga serie de posts que estoy dedicando al aprendizaje por refuerzo ('reinforcement learning'), nos habíamos quedado en el punto en que estábamos tratando con problemas en que ya usábamos redes neuronales como parte del algoritmo ('deep reinforcement learning') y que, además, nos enfrentábamos a un espacio de estados continuo, como el que ocurre, por ejemplo, en la locomoción de robots. 

Y habíamos pasado a trabajar directamente con políticas, desentendiéndonos de los valores. En este post vamos a avanzar sólo un poquito más, indicando una de las formas habituales en que se hace eso, utilizando, como es tan común en deep learning, el concepto de gradiente

Repasando

Antes de revisar las nuevas ideas, el repaso habitual, tomando como esquema la ya muy conocida figura:

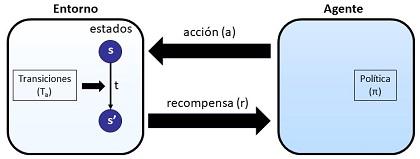
Nos encontramos ante la situación de un agente (por ejemplo un robot) que interacciona con un entorno. Ese entorno se encuentra en un estado s. La interacción del agente con el entorno se concreta en la ejecución por parte del agente de acciones, a. Como consecuencia de esas acciones, el entorno puede experimentar una transición a un nuevo estado s' y el agente recibir una recompensa r. El agente decide la acción a aplicar en cada momento, siguiendo una política π.

Lo que pretendemos en el aprendizaje por refuerzo es aprender la mejor política π, de forma que se maximice la recompensa acumulada.

Los algoritmos más básicos, con unos estados discretos y de número reducido en el entorno, utilizan mecanismos basados en tablas (algoritmos tabulares) en que, para cada estado, se obtiene un valor de recompensa acumulada. Hablamos de recompensa acumulada porque lo que se busca no es optimizar la recompensa ante una acción aislada, sino ante una secuencia de acciones. Esa secuencia de acciones y sus consiguientes transiciones de estados y recompensas constituye lo que se denomina una trayectoria y, al final, en una trayectoria, tendremos una recompensa acumulada.

Lo métodos tabulares, como decimos, establecen en una tabla, el valor de esa recompensa acumulada esperada, que se tabula por cada estado (V) o por cada estado-acción (Q).

Cuando la dimensión del problema es muy grande, dejamos de trabajar con estados, la situación del entorno la representamos por unas características y usamos redes neuronales para implementar las funciones de valor y la política, conduciendo al 'deep reinforcement learning'.

El último paso visto en el post anterior es cuando estamos en una situación con estados y acciones no discretos sino continuos. Y nos quedamos diciendo que, en esa situación, nos olvidamos de trabajar con esa función Q que nos daba la recompensa acumulada esperada para un estado-acción sino que trabajamos directamente con la política π

El esquema de funcionamiento

Siguiendo, como en toda esta serie de posts, lo indicado el  libro 'Deep reinforcement learning' de Aske Plaat, observamos que el esquema básico de funcionamiento en ese aprendizaje de una política en un problema continuo, se puede resumir en los siguientes pasos

• Inicializamos los parámetros θ de la política


• Hasta que se alcance la convergencia, repetimos
  
  • Muestreamos una nueva trayectoria τ
  
  
  • Si τ es una 'buena trayectoria', modificamos los parámetros θ en la dirección de 'acercarnos' a esa trayectoria. Si se trata de una 'mala trayectoria', por el contrario, modificamos los parámetros en el sentido de 'alejarnos' de esa trayectoria.

Claro, para que este esquema de algoritmo sea operativo, necesitamos alguna forma de ver eso de que una trayectoria 'es buena' o 'mala', es decir, necesitamos medir lo que se denomina la calidad de la política, J. Una forma posible de hacerlo es retornar a las funciones valor, V, y tomar como calidad de la política el valor de la política en el estado inicial, s0, según esa función V, lo que expresado matemáticamente sería

J(θ) = V^π(s₀)

Y, lógicamente, lo que queremos es maximizar esa calidad de la política. Suponiendo que esa calidad es una función diferenciable (cosa que ya se imaginará el lector vamos a buscar de forma explícita y que no sucederá por casualidad), lo que vamos a hacer es trabajar con el gradiente . El gradiente nos da la variación de esa función de calidad ante un cambio de parámetros. Matemáticamente, eso significa hacer unas derivadas parciales en cada una de las dimensiones pero, geométrica e intuitivamente, implica calcular y utilizar la 'inclinación' de la superficie definida por por la función calidad de la política y, formalmente, se expresaría como

∇_θJ(θ) = ∇_θV^π(s₀)

En cada iteración, ajustaremos los parámetros θ aplicando la sencilla fórmula

θ_t+1 = θ_t + α · ∇_θJ(θ)

Es decir, en cada paso, los parámetros se ajustan sumándoles el gradiente de la calidad de la política (es decir, cómo varía), multiplicados por un factor de aprendizaje, α, que es un número real positivo, con frecuencia comprendido entre 0 y 1.

Los lectores familiarizados con las matemáticas en general y con las matemáticas del machine learning y el deep learning en particular, seguramente ya habrán pensado en el algoritmo de descenso de gradiente, tan habitual, por ejemplo, en el aprendizaje de redes neuronales. Y habrán pensado bien porque, en efecto, esa es la idea, con la única sutil diferencia de que, mientras en el aprendizaje de deep learning habitual buscamos normalmente minimizar una función error, en este lo que queremos es maximizar esa calidad. Por ello, en lugar de un descenso de gradiente, usamos un ascenso de gradiente, pero la idea es prácticamente la misma.

Para resumir un poco la idea, lo que vamos a hacer es implementar la política como una red neuronal (recordar que ya estamos en 'deep reinforcement learning'), inicializar sus parámetros (sus pesos) de alguna forma, normalmente de manera aleatoria, y luego hacer un aprendizaje iterando por trayectorias y ajustando esos pesos mediante un ascenso de gradiente aplicado a la calidad de la política medida como el valor de esa política en el estado inicial.

Esta forma de actuar se utiliza, por ejemplo, en el método REINFORCE.

Otros métodos

En el libro citado, se mencionan y explican otras formas de  trabajar para optimizar esa política, como 'actor critic' o TRPO, pero no entraremos en ellos, al menos de momento, y sólo dejar constancia de que existen.

Conclusiones

Aunque hay varios métodos y algoritmos para conseguir trabajar en el caso de problemas continuos en la optimización directa de una política parametrizada, normalmente implementada como una red neuronal, hemos esbozado como se realiza aplicando el ascenso de gradiente sobre una calidad de política que se mide como el valor de esa política en un estado inicial.

Artículos de este blog relacionados

• Notas sobre aprendizaje por refuerzo (VIII): problemas continuos y métodos basados en políticas
• Notas sobre aprendizaje por refuerzo (VII): El triunfo del algoritmo DQN (Deep Q-Network)
• Notas sobre el aprendizaje por refuerzo (VI): los tres retos del deep reinforcement learning
• Notas sobre el aprendizaje por refuerzo (V): deep reinforcement learning
• Notas sobre aprendizaje por refuerzo (IV): Métodos tabulares. SARSA Y Q-Learning
• Notas sobre aprendizaje por refuerzo (III): recompensas, trazas y valores
• Notas sobre aprendizaje por refuerzo (II): Visualizando el aprendizaje en procesos de Markov
• Notas sobre aprendizaje por refuerzo (I): Procesos de decisión de Markov