Y damos un paso más en nuestro recorrido por las particularidades algorítmicas y técnicas del aprendizaje por refuerzo ('reinforcement learning').En este post vamos a introducir un pequeño cambio de tercio centrándonos en problemas en que el espacio de estados es continuo (y, por tanto, de alguna forma infinito), por lo que debemos cambiar la perspectiva y no basarnos en las funciones del estado, sino en las propias políticas.
¿Te suena extraño ese vocabulario, estimado lector?
Bueno, pues como en todos los posts anteriores de esta serie, vamos a hacer un breve repaso.
Recordatorio: Aprendizaje por refuerzo y deep reinforcement learning
Los seguidores de esta serie de posts ya conocen bien lo que viene a continuación:
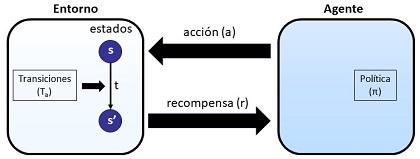
Nos hallamos ante problemas en que un agente interacciona con su entorno, aplicando unas acciones (a) y recibiendo unas recompensas (r) por ello. El entorno está definido por un estado (s) y, al recibir la acción a del agente, eventualmente se produce un cambio de estado a s', momento en que se genera la recompensa r. Para decidir qué acción aplicar en cada momento, el agente aplica una política π. Lo que queremos conseguir es que el agente aprenda la mejor política, aquella que maximice su recompensa acumulada (es decir, no la recompensa ante una acción concreta sino ante toda una serie de acciones que conduzcan, eventualmente a un estado final).
Los algoritmos que hemos visto hasta ahora, se apoyan en la implementación de unas funciones valor para un estado (V) o valor para un estado y acción dados (Q), que nos proporcionan, precisamente, la estimación de la recompensa acumulada.
En los algoritmos más sencillos, aquellos aplicables cuando el entorno exhibe un número finito y no muy alto de estados, utilizábamos un enfoque tabular, trabajando con tablas indexadas con base a estados.
Cuando la dimensionalidad del problema crecía mucho, es decir, el número de estados posibles era demasiado alto, teníamos que cambiar el enfoque. Y ese cambio de enfoque nos llevaba a renunciar a conocer los estados como tal y, en lugar de ello, caracterizar la situación del entorno mediante un conjunto de características. Además, pasábamos a implementar las funciones principales del problema, las funciones de valor y la política como redes neuronales profundas, llegando hasta el 'deep reinforcement learning'.
Robótica y espacios de estados continuos
Los algoritmos usados hasta ahora tienen sentido cuando los estados y las acciones posibles eson discretos y están claramente diferenciados. En ellos, las acciones disponibles están muy claras y podemos diferenciar de manera nítida entre la mejor acción y el resto.
Sin embargo eso no es así en muchos problemas del mundo real, problemas que además aplican a campos que son de mi muy especial interés como la robótica, los vehículos autónomos o los juegos de estrategia en tiempo real.
En concreto, los métodos que veremos, se aplican a robots que caminan o saltan, lo que se denomina 'locomoción'.
En concreto, en el conocido video que se muestra abajo, se ve a un agente, una especie de robot simulado, que aprende a correr y saltar mediante el tipo de algoritmos que en seguida veremos:
Métodos basados en política ('policy-based methods')
Para estos casos, tal y como se nos indica en el libro 'Deep reinforcement learning' de Aske Plaat, cuyo discurso estoy siguiendo en toda esta serie de posts, debemos cambiar el enfoque. Si hasta ahora nos enfocábamos en las funciones de valor de estado o de estado-accion, ahora abandonamos esas funciones y trabajamos directamente con la política a optimizar π
Estos métodos continúan apoyándose en soluciones de redes neuronales profundas que aprenden mediante el famoso algoritmo de descenso de gradiente.
Los tres métodos que menciona la obra mencionada son 'REINFORCE', 'Asynchonous advantage actor critic' y 'proximal policy optimization'.
Espacios de acciones continuos
En el tipo de problemas que estamos tratando, nos concentramos en las acciones, unas acciones que ahora se encuentran también en un espacio continuo. Así, el movimiento de la junta de un robot puede adoptar un valor continuo en radianes, al igual que lo puede hacer la posición del volante de un vehículo autónomo o el giro de sus ruedas.
Así, por ejemplo, y suponiendo que podemos girar una circunferencia completa, podríamos tener un valor contenido en el rango
[0,2π ] ∈ ℜ
donde existen un número de valores posibles infinito. Una opción podría ser discretizar estos valores. Sin embargo, los métodos de que nos ocupamos optan por trabajar directamente con acciones continuas y, por tanto, unas políticas que también son continuas.
Políticas estocásticas
Además, estos métodos utilizan unas políticas estocásticas que se traducen en distribuciones de probabilidad sobre las acciones.
Esta forma de actuar evita la inestabilidad en el caso de entornos estocásticos que aqueja a los métodos vistos hasta ahora basados en valor. Además, estas políticas incorporan 'de serie' el concepto de exploración' que vimos en el quinto post de esta serie cuando explicamos los algoritmos SARSA y Q-learning.
Conclusiones
De momento detengo aquí la exposición. Por supuesto, sólo hemos rascado un poco y delineado el tipo de problemas, algunos campos de aplicación y las bases de los algoritmos sin entrar a explicar con más detalle ninguno concreto, cosa que seguramente hagamos en un próximo post. Pero prefiero ir poco a poco, porque abordamos una temática bastante compleja.
Lo más interesante, es que nos estamos introduciendo ya en algoritmos muy cercanos a las complejas aplicaciones reales, más allá de los juegos y, en concreto, en elementos muy avanzados propios de la robótica o los vehículos autónomos, que me interesan especialmente.
Artículos de este blog relacionados
- Notas sobre aprendizaje por refuerzo (VII): El triunfo del algoritmo DQN (Deep Q-Network)
- Notas sobre el aprendizaje por refuerzo (VI): los tres retos del deep reinforcement learning
- Notas sobre el aprendizaje por refuerzo (V): deep reinforcement learning
- Notas sobre aprendizaje por refuerzo (IV): Métodos tabulares. SARSA Y Q-Learning
- Notas sobre aprendizaje por refuerzo (III): recompensas, trazas y valores
- Notas sobre aprendizaje por refuerzo (II): Visualizando el aprendizaje en procesos de Markov
- Notas sobre aprendizaje por refuerzo (I): Procesos de decisión de Markov
Puzzle Bobble
Karate Blazers
Puzzle De Bloques
Magical Cat Adventure