Han sido nueve días intensos de extraordinarias aportaciones. Algunas procedentes de participantes 'clásicos', otras de antiguos colaboradores a los que echábamos de menos, y algunas de nuevos seguidores.A tod@s vosotr@s, quiero daros las gracias por vuestra participación y por vuestro compromiso. Y también a todos los que no pudieron colaborar en el Carnaval, en su mayor parte por falta de tiempo.
Una vez concluido el periodo de presentación de artículos, ahora es tiempo de leerlos con calma y, sobre todo, de votar por las aportaciones que más os gusten.
Éstas son todas las entradas que he recopilado a lo largo de estos días en la presente Edición 6.7: El punto del Carnaval de Matemáticas:
Sábado, 17 de octubre
- Entrada 1. Pero, ¿queda algo por descubrir en Matemáticas? de MasScience.
Cristóbal inaugura el Carnaval mostrándonos que las matemáticas son una ciencia viva, con infinitas posibles cuestiones sobre las que investigar.
- Entrada 2. La teoría del punto gordo de from Cardescu Web.
Cristian nos recuerda la teoría del punto gordo, gracias a la cual muchos de nosotros aprobamos el dibujo técnico del antiguo BUP.
- Entrada 3. Ludos tonalis: simetría musical de ::ZTFNews.org.
Marta nos descubre una curiosa composición musical simétrica, corroborando una vez más la estrecha relación entre matemáticas y arte.
- Entrada 4. Biografía y obra de Mariano Mataix de Espejo Lúdico.
Juan Luis nos presenta a Mariano Mataix, el hombre de los mil y un pasatiempos numéricos, casi desconocido a pesar de que fue un inagotable escritor de matemáticas recreativas.
- Entrada 5. Sumar no es colocar un número debajo de otro de En el aula con Blanca.
Blanca nos plantea la necesidad de mejorar los métodos de enseñanza de las matemáticas, incidiendo en la comprensión de los algoritmos que utilizamos y no en su mera aplicación mecánica.
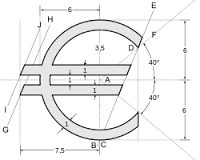
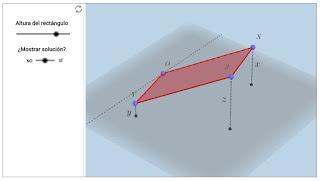
- Entrada 6. Un rectángulo de sobremesa de Tito Eliatron Dixit.
Tito nos brinda un problema matemático aparentemente sencillo a partir de una simple hoja de papel y una mesa, y con una solución inesperada.
- Entrada 7. Calendario matemático 2016: un reto diario de ::ZTFNews.org.
Marta nos informa de la publicación del calendario matemático del año 2016, lleno de nudos salvajes y de retos diarios para resolver.
- Entrada 8. Reseña: "La conferencia perdida de Feynman" y material adicional en Geogebra de MTH TICS.
David nos realiza una reseña del libro dedicado a la conferencia 'El movimiento de los planetas alrededor del Sol' impartida por el físico Richard P. Feynman, e ilustrado con material Geogebra.
- Entrada 9. Una nueva superficie K3 inspirada en los números taxicab de La Ciencia de la Mula Francis
Francisco nos describe la nueva superficie K3 elíptica descubierta recientemente por los matemáticos, denominada también 1729 en honor del número taxicab de Ramanujan.
- Entrada 10. Pásalo bien leyendo un libro de Mates de Mateblog
Mariló nos alienta a divertirnos con la multitud de viñetas divertidas sobre matemáticas que encontraremos en el libro 'Ríete con las Mates'.
- Entrada 11. La catenaria de PiMedios.
Jesús nos inicia en las fórmulas matemáticas correspondientes a las curvas que forman los cables y cadenas que cuelgan suspendidos por sus extremos.
- Entrada 12. Canciones matemáticas y su utilización en clase de Matemáticas recreativas y educativas.
Antonio nos recomienda la música como una estupenda manera de motivar a los alumnos y de introducir conceptos matemáticos de forma amena y práctica.
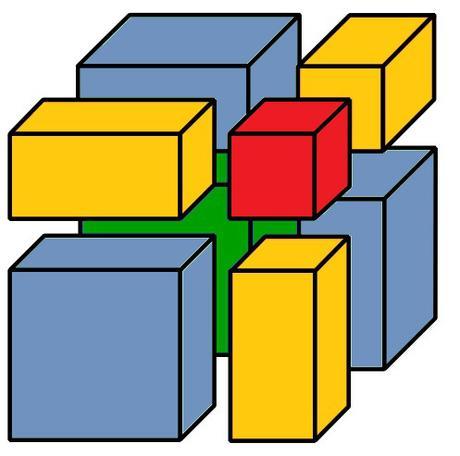
- Entrada 13. ¡Ya lo pensaba Euclides! Mejor lo dibujamos de Matemáticas cercanas.
Amadeo nos recrea una descomposición tridimensional del cubo de un binomio, que nos permite visualizar y entender mejor su desarrollo.
- Entrada 14. Yo de matemáticas fatal, señor agente de Cifras y teclas.
David nos desvela cómo es necesario dominar el mundo de las matemáticas para evitar las multas en los aparcamientos.
- Entrada 15. Shinichi Mochizuki y su demostración de la conjetura abc de La Ciencia de la Mula Francis.
Francisco nos introduce a Shinichi Mochizuki, una estrella japonesa de las matemáticas, de la que, hasta dentro de al menos 10 años, no sabremos si se trata de un genio o si está equivocado.
- Entrada 16. Callejero Matemático XIV Paseo Oliva Sabuco de Nantes de Los Matemáticos no son gente seria.
Juan nos explica quién fue Oliva Sabuco de Nantes, una científica española del siglo XVI poco conocida, y que da nombre a una de las calles de su barrio.
- Entrada 17. La probabilidad en el banquillo de los acusados de Cuaderno de Cultura Cientítica.
Raúl nos explica los peligros que tiene la incorrecta interpretación de la probabilidad en los juicios, que en ocasiones ha llevado a meter entre rejas a inocentes.
- Entrada 18. Fractales con piezas de cartulina de Juegos topológicos.
José Luis nos expone un recurso didáctico realizado con niños, consistente en la realización de una isla de Koch y de otras composiciones fractales con cartulinas.
- Entrada 19. Concurso de relatos cortos matemáticos π-ensa de Que no te aburran las m@tes.
Elisa nos propone una iniciativa para difundir las matemáticas en los institutos, a través de la convocatoria de un premio de relatos cortos matemáticos.
- Entrada 20. Los banderines de Euler de Matifutbol.
Herminio nos plantea un paseo por el mundo matemático de Euler, a partir de un enigma que la Asociación de Topólogos Anónimos ha formulado a Pepe Vitruvio.
- Entrada 21. Terence Tao demuestra la conjetura de la discrepancia de Erdős de La Ciencia de la Mula Francis.
Francisco nos presenta al matemático Terence Tao, al frente de los proyectos PolyMath mediante los que se ha conseguido la resolución colectiva de problemas matemáticos a través de la web.
- Entrada 22. Arcos de Málaga: deprimido cóncavo de El mundo de Rafalillo.
Rafael nos invita esta vez a conocer un nuevo tipo de arco, frecuentemente utilizado en arquitectura, con varios ejemplos del mismo encontrados en su ciudad.
- Entrada 23. Manchas solares de Pikasle.
Víctor nos anima a practicar la astronomía durante el día, único momento en que podremos observar (de forma indirecta, por favor) el astro rey.
- Entrada 24. 'Mi' cíclide de Dupin de ::ZTFNews.org.
Marta nos aporta un artículo sobre la cíclide de Dupin y el Encuentro de Topología para cerrar así su participación en este Carnaval dedicado al punto.
- Entrada 25. Vera, a ver si sabes decirme... de Matemáticas cercanas.
Amadeo nos guía desde el dibujo de un simple punto hasta la fórmula de Pick, repasando durante el camino el cálculo de las áreas de distintos polígonos regulares e irregulares.
- Entrada 26. Double Bubble de Tito Eliatron Dixit.
Tito nos descubre dos applets de Geogebra para que comprobemos la película de intersección que se forma entre dos pompas de jabón de distinto tamaño.
- Entrada 27. 72 lápices de Geometría dinámica.
Rafael nos revela cómo realizar construcciones geométricas sorprendentes y complejas con lápices, y las posibilidades didácticas que nos ofrecen.
- (Como puede que a Pepe Vitruvio se le haya escapado alguna publicación, no dudéis en escribirme para incluirla en este apartado lo antes posible.)
Ahora está en vuestra mano elegir la mejor entrada de este Carnaval. Ya sabéis que debéis votar tres entradas distintas, otorgando 4, 2 y 1 punto a cada una de ellas.Para ello, deberéis escribir un comentario al final de esta entrada. Como en anteriores ediciones, los comentarios no se publicarán hasta el término del periodo de votación.
En el caso de que desées votar, y no hayas participado con ninguna publicación, podrás hacerlo acompañando un enlace con tu perfil en la web del Carnaval de Matemáticas.
El plazo para las votaciones es desde la publicación de este resumen hasta el día 10 de noviembre.
Solo me queda expresar el enorme placer que me ha reportado la organización del Carnaval y la cálida respuesta que me habéis dispensado, y despedirme de tod@s vosotr@s hasta la siguiente edición, que albergará el blog Gaussianos.
¡Un abrazo!.
Puzzle Bobble
Karate Blazers
Puzzle De Bloques
Magical Cat Adventure