¿Sabías qué? – “Fibonacci” #MiércolesdeCiencia

La sucesión de Fibonacci es una secuencia de números enteros descubierta por matemáticos hindúes hacia el año 1135 y descrita por primera vez en Europa gracias a Fibonacci (Leonardo de Pisa).

La sucesión se describe de la forma siguiente:

F(0) = 0;
F(1) = 1;
F(n) = F(n-1) + F(n-2)

Lo que da la Serie siguiente:

 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597

Aparte de que esta sucesión tiene varias propiedades interesantes, como que se puede formar cualquier número natural mediante la suma de términos de la sucesión, sin que ninguno se repita, lo más curioso de esta sucesión es su presencia en la naturaleza.

La sucesión de Fibonacci está muy ligado a muchos aspectos de nuestra vida cotidiana como lo siguientes hechos:

• En las espirales de los girasoles.
• En las espirales de las piñas.
• El número de pétalos de una flor es generalmente un término de Fibonacci. Hay flores con 2 pétalos, 3, 5, 8, 13, 21, 34, pero muy rara vez es un número que no esté en esta sucesión.
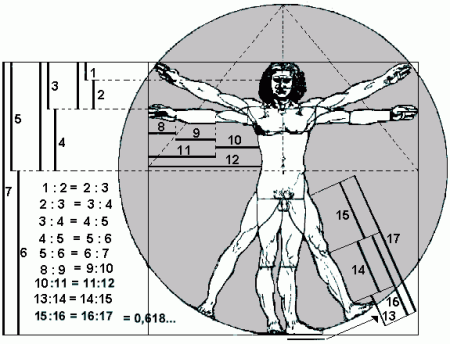
• En la relación entre la altura de un ser humano y la altura de su ombligo.
• La relación entre la altura de la cadera y la altura de la rodilla.
• En la mano humana también se encuentra esta recurrencia, la longitud del metacarpo es la suma de las dos falanges proximales y la longitud de la primera falange es la suma de las dos falanges distales.

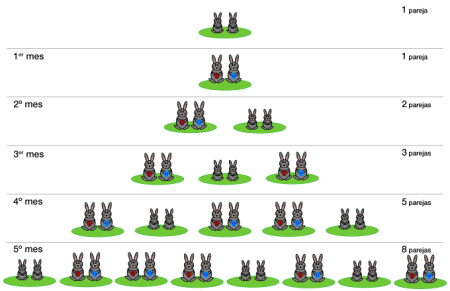
Y el ejemplo más claro y básico de todos es:

Los machos de una colmena de abejas tienen un árbol genealógico que cumple con esta sucesión.

Los zánganos, el macho de la abeja, no tiene padre (1),

pero sí que tiene una madre (1, 1),

dos abuelos, que son los padres de la reina (1, 1, 2),

tres bisabuelos, ya que el padre de la reina no tiene padre (1, 1, 2, 3),

cinco tatarabuelos (1, 1, 2, 3, 5),

ocho tataratatarabuelos (1, 1, 2, 3, 5, 8)

y así sucesivamente, cumpliendo con la sucesión de Fibonacci.

De hecho el Numero Áureo viene de esta sucesión y este grandioso número, nos da las pautas tanto para el Diseño Gráfico como para las Artes, lo podemos ver en las Pinturas, dibujos, Diseños, etc.

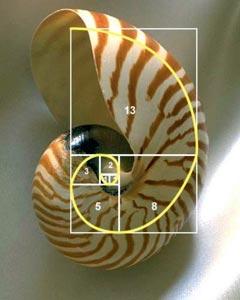
Como pueden ver siempre hay números y Matemáticas en TODOS lados ñ__ñ