Sistema de Numeración Problema resuelto

Problema
Realizar las siguientes conversiones:
a) 1238 al sistema binario.
b) 10101012 al sistema octal.
c) BACA16 al sistema binario.
d) 10101012 al sistema hexadecimal.
e) 1316310 al sistema binario.

Sug. Usar divisiones sucesivas y descomposición polinómica. T.
Solución
Presentamos 2 formas de resolver este problema.
a)
Primera Forma: Digamos que esta la forma trivial de realizar este proceso.
Convertimos el número 1238 a un número en base 10 (la que usamos),a través de la descomposición polinómica de la siguiente forma:
\( 123_8 = 1 \times 8^2 + 2\times 8^1 + 3 \times 8^0 \)
\( \rightarrow 1 \times 64 + 2\times 8 + 3 \times 1 \)
\( \rightarrow 83\)
Luego convertimos el número 83 a un número en base 2 (binario) a través de divisiones sucesivas:

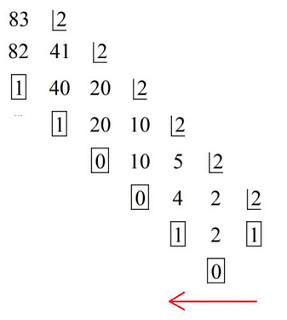
Procedemos a escribir los números que se encuentran encerrados en un cuadrado, empezando con el número que se encuentra en la parte izquierda para terminar con la que se encuentra en la parte derecha obteniendo así el número en base 2, es decir:
\( 83 = 83_{10} = 1010011_2 \)
Luego diremos que el número 123 en base 8 es equivalen al número 83 en base 10 y estos a su vez son equivalentes al número 1010011 en base 2.
Segunda Forma
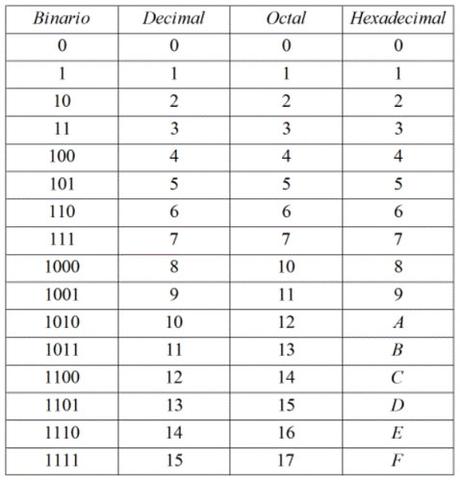
Examinemos la siguiente tabla, nos muestra números en el sistema decimal(de base 10), en el sistema octal(base 8) y en el sistema binario(base 2).

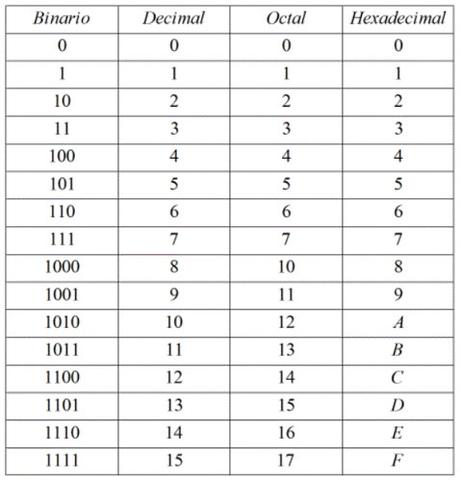
Vemos las equivalencias entre los valores de los distintos sistemas de numeración, por ejemplo el número 5 en base 10 es equivalente al número 5 en base 8(octal) y a su vez estos son equivalentes al número 101 en base 2(binario).
Cuando queramos convertir un número de base 2 a base 8 o viceversa es conveniente expresar los números de base 2(sistema binario) como números de 3 cifras como en la tabla.
Según la tabla vemos que 1 en base 8 es equivalente a 001 en base 2; 2 en base 8 es equivalente a 010 en base 2 y 3 en base 8 es equivalente a 011 en base 2.
Ahora solo reemplazamos las equivalencias anteriores en el número 1238, obtenemos:
\( 123_8 = 001 010 011_2 \)
Despreciando los ceros de la izquierda del número anterior que esta en base 2, tenemos:
\( 123_8 = 1010011_2 \)

b)
Primera Forma: Una forma trivial de realizar este proceso.
Convertimos el número 10101012 a un número en base 10 , de la siguiente forma:

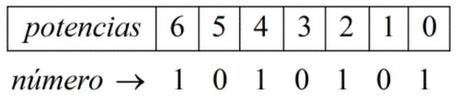
\( 1010101_2 = 1 \times 2^6 + 0 \times 2^5 + 1\times 2^4 + 0 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 \)
\( 1010101_2 = 64 + 16 + 4 + 1 = 85 \)
Luego convertimos el número 85 a un número en base 8 a través de divisiones sucesivas:

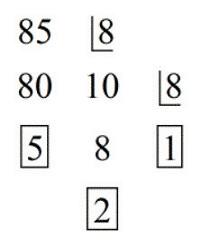
Procedemos a escribir los números encerrados en un cuadrado, empezando de la izquierda hacia la derecha, obteniendo el número en base 8, es decir:
\( 85 = 85_{10} = 125_8 \)
Segunda Forma
Usamos nuevamente la tabla que vimos anteriormente:

Separamos en grupos de 3 cifras de derecha a izquierda al número de base 2. Se forman 2 grupos de 3 cifras y un grupo incompleto de una sola cifra, completamos con ceros este grupo(números de color rojo).

Miramos la tabla y notamos que el número 001 en base 2 es equivalente al número 1 en base 8, el número 010 en base 2 es equivalente a 2 en base 8 y el número 101 es equivalente a 5 en base 8.
Ahora solo reemplazamos las equivalencias anteriores al número 10101012 Obtenemos el número equivalente en base 8.
\( 125_8 = 1010101_2 \)

c)
Veamos la siguiente tabla

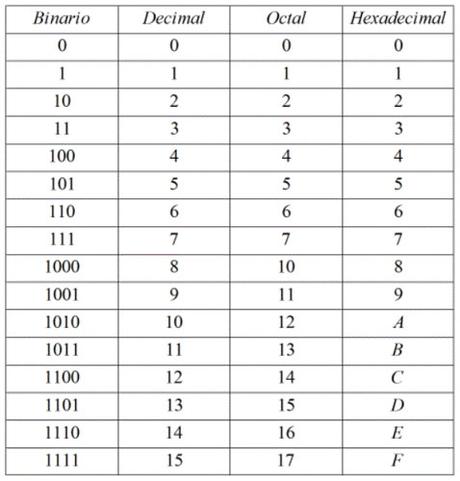
Nos muestra las equivalencias entre los valores de los distintos sistemas de numeración.
Luego procediendo como en la segunda parte de a), tendremos:

Acomodando los números y haciendo un simple reemplazo convertimos un número de base 16 a base 2.
\( BACA_{16} = 1011101011001010_2 \)
d)
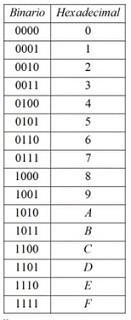
Tener en cuenta la siguiente consideración: Cuando queramos convertir un número de base 2 a base 16 o viceversa es conveniente expresar los números de base 2(sistema binario) como números de 4 cifras como en la tabla anterior.
Luego procediendo como en la segunda parte de b), solo que esta vez formamos grupos de 4 cifras de derecha a izquierda completando con ceros el grupo incompleto, tendremos:

Luego
\( 1010101_2 = 01010101_2 \)
Considerando el cuadro y la expresion anterior
\( 1010101_2 = 0101\) \(0101_2 = 55_{16}\)
En una línea queda resuelta el ejercicio.

e)
Primera Forma
Usamos divisiones sucesivas para convertir el número a base 2.

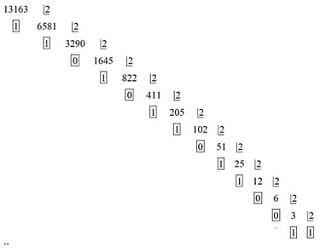
Es decir el número 13163 en base 2 es:
\( 13163_{10} = 11001101101011_2\)
Segunda Forma
Convertimos el número a base 8.

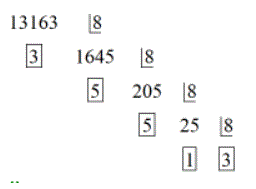
\( 13163_{10} = 31553_8\)
Usamos lo aprendido en la segunda parte de a) y obtenemos:
\( 13163_{10} = 3\) \(1\) \(5\) \(5\) \(3_8\)
\( 13163_{10} = 011\) \(001\) \(101\) \(101\) \(011_8\)
\( 13163_{10} = 11001101101011_8\)
En la primera forma de solución utilizamos 14 divisiones engorrosas que nos demoran y en las que nos podemos equivocar, en la segunda forma utilizamos solo 3 divisiones ahorramos tiempo y tenemos menos probabilidad de equivocarnos al encontrar la respuesta final.
Nota importante
Es posible usar los métodos aprendidos al convertir un número de base 2 a base 8 o viceversa o de base 2 a base 16 o viceversa, en los demás sistemas de numeración no funcionan estos métodos.
Notamos que la 2da forma es la más directa, rápida y confiable.