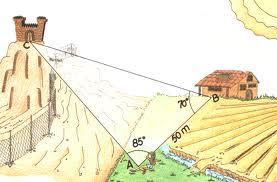
¿Cuál sería la distancia de la casa al castillo?
Actividad 1. Medir al altura de una montañaResuelve este problema.“En la llanura, desde un punto de cualquiera, se mide el ángulo B de elevación y se obtiene 43º, tras acercarnos a la montaña 200 m, se vuelve a medir el ángulo C de elevación y se obtiene 52º. Halla la altura de la montaña”
PASOS
- En la barra de menús, Elige Visualiza y desactiva la opción Ejes
- En el campo de entrada, introduce d = 2 (luego habrá que multiplicar por 100)
- Introduce también α = 43º y β = 52º
- Elige segmento dados su longitud y punto extremo inicial. Haz clic en el punto A. En la ventana que aparece, escribe d y haz clic en el botón aplicar
- En el menú Contextual de la letra a, elige propiedades/básiico/expone rótulo y selecciona nombre & valor
- Dibuja la semirrecta AB
- Elige ángulo dada su amplitud. Haz clic en el punto B y en el punto A. En la ventana que aparece, introduce α y haz clic en el botón aplicar
- Dibuja la semirrecta AC
- Dibuja el punto D de la semirrecta AB
- Dibuja el ángulo β = 52º
- Halla el punto de intersección de c y e, se obtiene el punto F
- Dibuja un recta perpendicular desde el punto F a la semirrecta horizontal
- Halla el punto de intersección de la recta perpendicular con la semirrecta horizontal
- Desactiva Expone objeto de la recta perpendicular
- Dibuja el segmento GF, renómbralo como h y que se vea el nombre & valor
- Dibuja el segmento BG y que se vea el nombre & valor
Actividad 2. Circunferencia circunscritaComprueba que se cumple la propiedad que muestra el teorema de los senos de que el cociente entre el lado de un triángulo y el seno del ángulo opuesto es igual a 2 veces el radio de la circunferencia circunscrita.
PASOS.
- Dibuja un triángulo ABC
- Expón la medida de sus lados
- Dibuja sus ángulos
- Elige Dibujar Mediatriz y traza las mediatrices de los tres lados y marca el circuncentro
- Dibuja la circunferencia circunscrita
- Dibuja un diámetro y muestra su valor
- Oculta las mediatrices
Actividad 3. Resolver un triángulo. Caso 2 (dos posibles soluciones)Resuelve un triángulo en el que se conocen a = 6,2 b = 7,4 A = 48º
PASOS
- Introduce los valores de a, b y A
- Dibuja el segmento b
- Dibuja el ángulo A
- Dibuja una circunferencia de centro C y radio a
- Halla la intersección de la semirrecta con la circunferencia
- Oculta todo lo que no necesites
- Dibuja los triángulos CBE y CBF
- Dibuja los ángulos de los dos triángulos CBE y CBF
- Muestra el área
PASOS
- Elige visualiza y desactiva la opción ejes
- Elige Semirrecta que pasa por dos puntos y haz clic en el origen A y en otro punto B para indicar la dirección
- Dibuja la semirrecta AC
- En el menú contextual de cada lado, desactiva la opción expone rótulo
- Desactiva también el rótulo de la semirrecta oblicua
- Elige Ángulo, y haz clic sucesivamente en B, A y C
- Elige Nuevo punto y haz clic en el punto D del lado AB
- Selecciona Recta perpendicular, haz clic en el punto D y en la semirrecta horizontal
- Elige Intersección de objetos y haz clic en la recta perpendicular y en el lado oblicuo AC, se obtiene el punto E
- En el menú contextual de la recta perpendicular desactiva Expone objeto
- Elige segmento entre dos puntos y haz clic en D y en E
- En el menú contextual de este segmento, elige Renombra, ponle b
- En el menú contextual del segmento DE elige Propiedades, en la ficha Básico escoge Expone Rótulo/Nombre & Valor, en color pónle color rojo, en Estilo elige groso 4
- Dibuja el segmento AE, renómbralo como a
- Elige Copiar estilo visual y haz clic en el segmento b y luego en a
- Elige Insertar texto y haz clic en un punto de la pantalla y escribe “sen” + α + “ = “ + sin(α)
- En el menú contextual del texto , pestaña texto, elige el tamaño 18, negrita y en Color azul. Lleva el texto a la parte superior izquierda
- Debajo inserta el texto “b/a = ” + b + “/” + a + “ = “ + b/a
Actividad 5. Interpretación del signo de una razón trigonométricaEn esta actividad vemos como el seno es positivo en los dos primeros cuadrantes y negativo en el dos siguientes
PASOS
- En la barra de menús, elige Visualiza y activa la opción Ejes
- Selecciona Desplaza. Pulsa la tecla control y arrastra el origen de coordenadas al centro de l pantalla
- Dibuja el ángulo BAC
- Elige Insertar texto haz clic en un punto de la pantalla y escribe “sen ” + α + “ = ” +sin( α)
Ejercicios sacados del libro de 1º Bachillerato de Editorial Bruño
