Trigonometría Problema resuelto

Problema
A ambas orillas de un río crecen dos palmeras, una frente a la otra. La altura de una es de 30 metros y la de la otra es 20 metros. La distancia entre sus troncos es 50 metros. En la copa de cada palmera hay un pájaro. De súbito los dos pájaros descubren un pez que aparece en la superficie del agua, entre las dos palmeras. Los pájaros se lanzaron y alcanzaron el pez al mismo tiempo.
¿A que distancia del tronco de la palmera mayor apareció el pez?


Sug. Considerar misma rapidez de vuelo.

Solución
Según el gráfico consideramos que inicialmente los pájaros estaban en los puntos \(B\) y \(E\) y dado que los pájaros alcanzaron el pez al mismo tiempo, asumiendo que ambos tuvieron la misma rapidez de vuelo concluimos que ambos recorrieron la misma distancia para alcanzar el pez, por tanto del gráfico consideramos que \(BC = CE\)

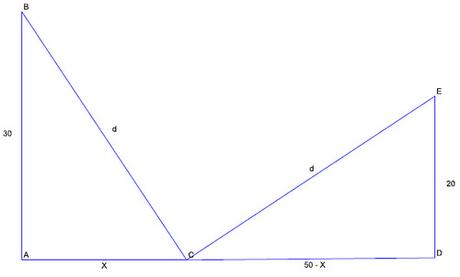
Aplicando el Teorema de Pitágoras en los triángulos \(ABC\) y \(CDE\):
\(30^2+x^2=d^2\)
\((50-x)^2+20^2=d^2\)
Es decir:
\(30^2+x^2=(50-x)^2+20^2\)
Resolviendo la ecuación se obtiene que \(x=20\) metros.
Se observa que los dos triángulos \(ABC\) y \(CDE\) son congruentes.