Un punto de apoyo para Arquímedes

Cuando el gran Arquímedes dijo (según lo registró Pappus) "Dadme un punto de apoyo y moveré el mundo", no estaba diciendo algo tan descabellado como parece: Si hubiera conseguido ciertos elementos de calidad, en algún mercado de materiales de Alejandría abierto a medianoche, tal vez habría podido mover la Tierra. Con una tabla muy muy muy muy muy resistente y una masa equivalente a la del planeta, pero comprimida en una cómoda -aunque no muy manuable- bola de unos pocos metros lo habría logrado.
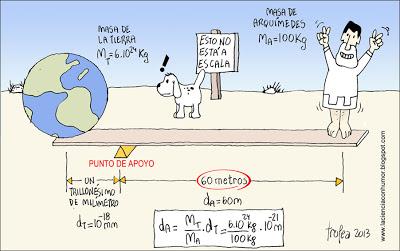
Veamos como sería eso: Arquimedes colocaría la masa en la tabla lo más cercana posible al punto de apoyo y él se pararía en el lado opuesto, para compemsar con la distancia y con su propio peso.
Claro, Arquímedes debería tener la habilidad y el pulso suficientes para poder posar sobre la tabla la enorme masa, tan pesada como la Tierra, a una distancia del punto de apoyo tal que no lo obligara a alejarse más allá de... digamos... el sistema solar. Por ejemplo, si Arquímedes lograra colocarla a una distancia de un trillonésimo de milímetro del punto de apoyo, entonces a él mismo, con su masa de 100 Kg, le bastaría con ubicarse a "sólo" 60 metros para equilibrar semejante masa planetaria. Una vez logrado eso, mover el mundo es un juego de niños nerd, el desafío de Arquímedes hecho fácil... bueno, al menos fácil teóricamente. Pero para qué seguir con aburridas explicaciones, si para entenderlo mejor arriba está el dibujito.
Sobre la forma de calcular la distancia: A la expresión final del recuadro que se puede ver en la viñeta se llega después de considerar inicialmente la ley de la palanca, que dice que La "potencia" por su brazo es igual a la "resistencia" por el suyo. Esto es, la proporción inversa entre la "potencia" (peso de Arquímedes) y su brazo por un lado y la "resistencia" (peso de la "Tierra") y el suyo por el otro. Para una "resistencia" dada, aumentos de la "potencia" obligan a disminuir su brazo, mientras que aumentos del brazo de potencia supondrán reducciones de su intensidad.. Al simplificar la aceleración de la gravedad en las expresiones de la potencia y la resistencia, los pesos han sido sustituidos por las respectivas masas, o dicho de otra manera,: la relación entre los pesos es igual a la relación entre las masas.