Viernes especial. La paradoja de los números interesantes

Todos los días que pasan desapercibidos tienen un encanto: una conversación, una discusión, un abrazo. Esto lo sabía bien Ramanujan.
Hoy es un día especial. Aunque no es Navidad, ni el día de los enamorados, ni entra la primavera, ni es el día de todos los santos, ni es fiesta nacional. Ni falta que le hace.
Y es que ni el día de Navidad nacen más niños, ni el día de los difuntos muere más gente, ni el día de los enamorados surgen más parejas.
Podríamos decir que hoy es uno de esos días perdidos en el calendario, y que, pese a ello, y también probablemente gracias a ello, puede resultar un día mágico.
Todos los días que pasan desapercibidos tienen un encanto: una conversación, una discusión, un abrazo. Esto lo sabía bien Ramanujan.
Srinivasa Aiyangar Ramanujan fue, probablemente, el matemático más importante del siglo XX, a pesar de morir víctima de la tuberculosis, con sólo 32 años. Nació en la India un 22 de diciembre del año 1887 y desde muy pequeño demostró una habilidad sorprendente para las matemáticas.

En 1912, se animó a enviar cartas con sus fórmulas y teoremas a varios matemáticos importantes del Reino Unido. Ninguno le prestó atención, salvo el profesor Harold Hardy de Cambridge.
Cuando Hardy leyó los escritos de Ramanujan se dio cuenta de su enorme talento y de sus cualidades excepcionales. Según sus palabras, aquellos escritos que el matemático indio le había enviado eran extraordinariamente enrevesados y complejos, y tanto si eran correctos como si no (de hecho, posteriormente se averiguó que algunos eran incorrectos), mostraban la imaginación increíble de su creador, y una asombrosa capacidad de deducción y análisis.

En realidad, Ramanujan afirmaba que sus teoremas estaban directamente inspirados por la diosa Namagiri mientras dormía, lo cual explicaría su bella confección y el infinito ingenio necesario para poder tan sólo imaginarlos.
Hardy le invitó a que fuera a Inglaterra, convirtiéndose en su amigo y mentor, y consiguiendo que fuese el primer ciudadano indio admitido en la Royal Society de Londres y en el Trinity College. Hasta su pronta muerte, trabajó sobre todo en la teoría analítica de los números, especialmente el número pi, el número e, y los números primos.

Una de las veces que Ramanujan estuvo ingresado en un hospital, recibió la visita de Hardy. Éste entró en la habitación desilusionado por el número de la matrícula del taxi en el que había llegado, el 1729, ya que le pareció muy insulso.
Ramanujan pensó unos segundos en lo que le había referido Hardy, y le contestó de inmediato que el 1729 era un número muy interesante, puesto que es el número más pequeño que puede ser expresado como suma de dos cubos de dos formas distintas: 1.729 = 1³ + 12³ = 9³ + 10³. Esto hace del número 1729 un número muy especial, que desde entonces se conoce como número de Hardy‑Ramanujan.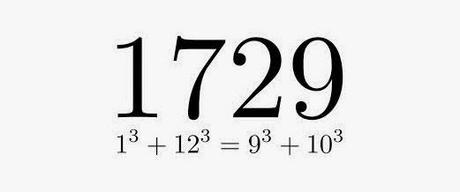

Lo más importante de esta anécdota es que constituye el origen de la paradoja de los números interesantes. Calificar a un número como interesante o aburrido es algo totalmente subjetivo. ¿Son más interesantes los números pares o los impares? ¿Los números primos o los compuestos?  ¿Son interesantes los números vampiro, o los números alegres, o los números triangulares, por el simple hecho de serlo?
Además, para todos y cada uno de ellos podremos encontrar alguna propiedad única o característica especial. Y si hay alguno para el cual no encontramos ninguna particularidad especial, entonces determinaremos que es el número aburrido más pequeño, y por ese mismo motivo se convertirá en un número interesante.

Esta paradoja de los números interesantes sin duda la podemos aplicar al resto de aspectos de nuestra vida.  Todas las personas y todos los días pueden ser únicos, y si no lo son por nada en particular, tendrán el aliciente de ser especiales por su normalidad y rutina.
¡Que paséis un excelente viernes y un no menos mágico sábado, en el que celebraremos el día pi (3/14)!
Agradecimiento: a Don Gabriel, inspirador de este relato.

Y si os gustó la historia, puedes difundirla a través de cualquiera de las redes que te propongo a continuación: