Pues bien, como veo que a la gente sí le ha gustado que trate temas matemáticos, os dejo con el “examen final” sobre el tema de inecuaciones lineales. Podéis dejar vuestras respuestas en el hilo, como siempre. Ya la semana que viene entraré en temática política, para variar y porque hay mucho más que decir sobre lo que ha ocurrido en los últimos días. Las agresiones del capital no pueden quedar impunes y el mundo está despertando cada vez más sobre el absoluto FRACASO DEL SISTEMA NEOLIBERAL REPUGNANTE que esclaviza a millones de seres humanos en el planeta. Me ha animado mucho ver la cantidad de jóvenes aquí que están rechazando los esquemas de las doctrinas neoliberales y que abogan por mayor solidaridad, igualdad, estado, y SOCIALISMO. Recordad siempre las palabras de Indalecio Prieto: “SOCIALISTA A FUER DE LIBERAL”. No se puede ser auténticamente liberal sin ser socialista y vice versa.
Aquí va el exámen final sobre los temas tratados en los últimos días.
————————————————————————————————————–
1) ¿Qué valores de “r” satisfacen la inecuación
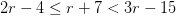
2) ¿Qué valores de "x" satisfacen la inecuación
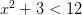
3) ¿Qué número es mayor:
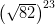
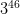
4) Supongamos que
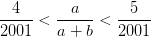
Computa el número de valores integrales que

5) Tiene
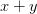
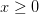
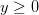
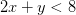
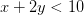
6) Consigue el valor máximo posible para

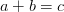
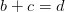
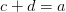
7) Para x, y, z, y w, y
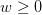
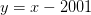
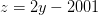
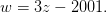
8) Busca el número entero menor que
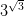
FIN DEL EXAMEN
