ANOVA - Análisis de varianza de un factor en R Studio.

¿Qué es ANOVA o Análisis de Varianza?

El análisis de varianza de un factor es una prueba paramétrica que se utiliza para comparar varios grupos o categorías (3 o más) en una variable cuantitativa y determinar si es que existen diferencias estadísticamente significativas entre las medias de aquellos grupos.

¿Qué necesito para realizar un ANOVA - Análisis de varianza de un factor?

Para realizar un ANOVA (Analysis of Variance) de un factor se requiere: una variable dependiente cuantitativa que es la variable objeto de medición y un factor o variable independiente cualitativa de agrupación que representa a los diferentes grupos o categorías. Además, este modelo estadístico requiere el cumplimiento de varios supuestos: 

• Independencia: las k muestras deben ser independientes, lo cual está relacionado al diseño del experimento a medirse y generalmente se acepta como cumplido si se han obtenido muestras aleatorias independientes dentro de cada uno de los grupos.
• Normalidad: la variable dependiente debe estar distribuida normalmente en cada grupo o categoría, lo cual puede probarse realizando el test de Kolmogorv-Smirnov, a través de gráficos Q-Q o incluso empleando gráficos de cajas.

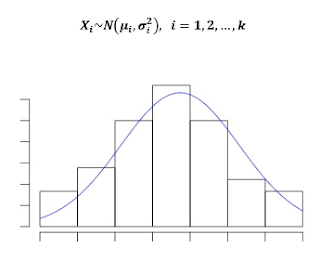
• Homocedasticidad: La variabilidad debe permanecer constante a través de los distintos grupos o categorías.

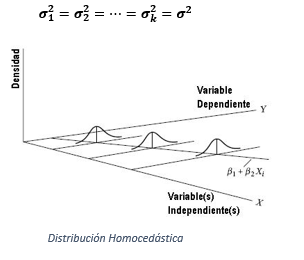
Hipótesis de un ANOVA 

El modelo se basa en la comparación de la variabilidad (varianza) que existe entre las medias de los grupos y la media dentro de los grupos para determinar si dichos grupos son más distintos entre sí que dentro de sí. Por lo que al final, las hipótesis a contrastar estarán dadas por:

Cómo podemos observar, de rechazar la hipótesis nula en favor de la alternativa, ANOVA sólo nos indica que existen al menos dos grupos o categorías que son diferentes entre sí y no permite identificar que grupos específicos son diferentes. Para ello, se pueden realizar pruebas de comparación múltiple post hoc como por ejemplo el Test de Tukey. 
El estadístico de contraste para esta prueba, está dado por:
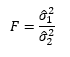Donde, el numerador es una estimación de la varianza poblacional basada en la variabilidad existente entre las medias de cada uno de los grupos y el denominador es una estimación de la varianza poblacional basada en la variabilidad existente dentro de cada grupo. Por tanto, cuanta mayor variabilidad exista entre las medias de cada grupo y la media dentro de los grupos mayor será el valor de F, lo que indicaría que las medias serán diferentes y se rechazaría la hipótesis nula.

Ejemplo práctico de un ANOVA - Análisis de varianza de un factor.

Para este ejercicio utilizaremos el archivo hsb2.xlsx, es una base de datos que contiene 200 observaciones tomadas aleatoriamente a estudiantes y que registran datos sobre género, edad, nivel socio-económico, notas de materias, etc. La práctica consistirá en realizar, utilizando el software R-Studio, un análisis ANOVA entre el estrato social y la puntuación obtenida en la evaluación de lectura, esta prueba utilizará un nivel de significancia de 0.05. A continuación, se muestra una descripción de las variables de la base de datos mencionada: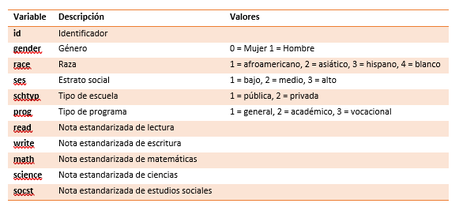

Como mencionamos anteriormente, para realizar una prueba ANOVA se deben cumplir con los siguientes supuestos:

• Independencia: dado que estamos usando datos que no hemos recolectado debemos confiar en que han sido tomados aleatoriamente.
• Normalidad y homocedasticidad: para demostrar estos supuestos vamos a utilizar un gráfico de cajas o boxplot, para lo cual vamos a utilizar los siguientes comandos en R:

Donde hsb2$read es la variable dependiente y hsb2$ses es la variable independiente.
Con dichos comandos obtendremos el siguiente gráfico:

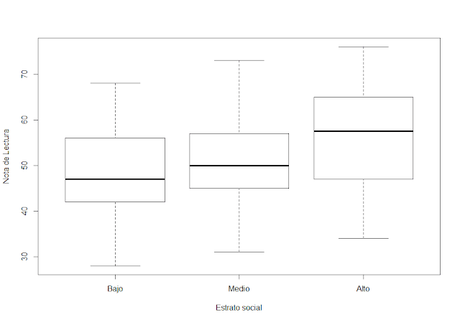
Para detectar normalidad debemos observar que la caja se encuentre hacia el centro de los límites y como podemos ver, cada uno de los estratos cumple (aunque no exactamente), con dicho criterio.En el caso de homocedasticidad, los datos deben mantener la misma variabilidad, es decir, deben mantener la misma dispersión. Para ello debemos observar que el tamaño de las cajas o rango intercuartílico se mantenga aproximadamente igual en cada uno de los grupos. En el boxplot podemos ver que el estrato social alto presenta una proporción un tanto mayor que los otros dos estratos pero que pudiese no ser tan significativa.
En conclusión, podemos afirmar que se cumplen los supuestos para poder realizar un análisis de varianza. 
Ahora procedemos a establecer las hipótesis:

Para mantener el contexto, vamos a calcular los promedios de la nota estandarizada de lectura para cada uno de los grupos, para ello utilizaremos los siguientes comandos:

Con lo que obtenemos la siguiente salida:

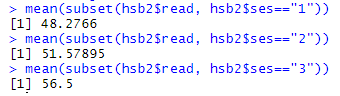
En resumen, obtenemos los siguientes valores:

Estos valores suponen que a medida que el estrato social es mejor el promedio de las notas de lectura también serán mayores. Con el análisis de varianza es justamente lo que se busca comprobar, si se rechaza la hipótesis nula en favor de la alternativa entonces se puede afirmar que si existen diferencias estadísticas significativas para concluir que los promedios son diferentes en función de un mejor o peor estrato social. Es decir, se afirmaría que a mejor estrato social el estudiante tendrá una mejor calificación en lectura. 
En R – Studio, procedemos a ejecutar los siguientes comandos para obtener el ANOVA:

Y obtenemos el siguiente resultado:

De esta tabla podemos observar que el estadístico de prueba F = 9.456, el cual es diferente de 1 y que el valor-p = 0.00012 el cual es menor al nivel de significancia definido previamente, esto es 0.05 .
Dado que , se rechaza la hipótesis nula en favor de la alternativa entonces se puede concluir que los promedios de los estratos sociales si son diferentes.
Ahora, lo que no dice el ANOVA es, cuales de los promedios difieren entre sí. Para ello podemos utilizar el test de Tukey para determinar entre que grupos hay diferencias significativas.
Ejecutamos el siguiente comando:
TukeyHSD(anova) -> anova es la variable donde se almacenó los resultados.
Y obtenemos la siguiente salida:
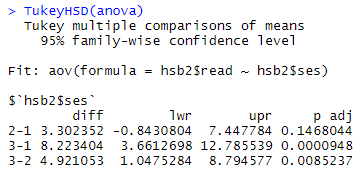Recordemos que los valores de la variable ses (estrato social) están dados por:
1 = bajo, 2 = medio, 3 = alto.
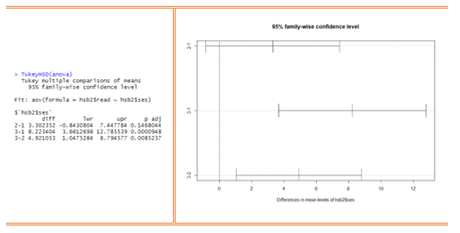
Este resultado muestra la diferencia entre los promedios (diff), los límites de los intervalos de confianza (lwr – upr), así como el valor-p (p adj) de cada una de las combinaciones en pares de los diferentes grupos de estratos sociales. 
El valor diff de la primera fila indica que la diferencia entre el promedio de las notas estandarizadas entre los estratos sociales bajo y medio es de 3.302352 con un valor-p = 0.1468044 el cual es mayor al nivel de significancia establecido 0.05, por lo que se puede afirmar que los datos no aportan información suficiente para concluir que existen diferencias entre los promedios, es decir, no se puede afirmar que un estudiante de estrato social medio tenga una mayor puntuación en la prueba de lectura que un estudiante de estrato social bajo.
El valor diff de la segunda fila indica que la diferencia entre el promedio de las notas estandarizadas entre los estratos sociales alto y bajo es de 8.223404 con un valor-p = 0.0000948 el cual es menor al nivel de significancia establecido 0.05, por lo que se puede concluir que si existen diferencias entre los promedios, es decir, se puede afirmar que un estudiante de estrato social alto obtuvo una mayor puntuación en la prueba de lectura comparado a un estudiante de estrato social bajo.
El valor diff de la tercera fila indica que la diferencia entre el promedio de las notas estandarizadas entre los estratos sociales alto y medio es de 4.921053 con un valor-p = 0.0085237 el cual es menor al nivel de significancia establecido 0.05, por lo que se puede concluir que si existen diferencias entre los promedios, es decir, se puede afirmar que un estudiante de estrato social alto obtuvo una mejor puntuación en la prueba de lectura comparado a un estudiante de estrato social medio.
Estas conclusiones podemos verlas gráficamente en R – Studio, para lo cual tenemos que hacer uso del siguiente comando:
plot(TukeyHSD(anova))

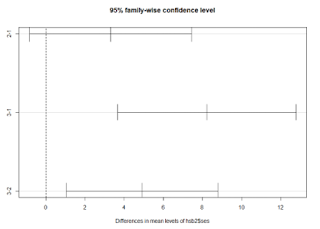
En este gráfico, los intervalos de confianza deben estar a la derecha o a la izquierda del valor 0 para que los promedios de dichos grupos sean diferentes, los intervalos de confianza que atraviesan el valor 0 no son estadísticamente significativos. Gráficamente podemos observar que el intervalo de confianza para los estratos 2-1 (medio – bajo) cruzan el valor 0 por lo que no se puede afirman que existan diferencias entre los promedios, en tanto que, los intervalos de confianza para los estratos 3-1 (alto – bajo) y 3-2 (alto – medio) se encuentran a la derecha del valor 0 por lo que se puede afirmar que si existen diferencias significativas en los promedios de dichos estratos, lo que corrobora las conclusiones expuestas en la tabla correspondiente al test de Tukey.

Si necesitas clases, realizar análisis de datos, resolución de guías de estudio, software o realizar algún proyecto que implique estadística, SPSS, Minitab, Excel, R, etc., puedes contactarme al 0960836772. 
Si deseas descargar este post, en la zona de descargas encontrarás un link con el documento en pdf y el archivo en excel que hemos utilizado para realizar el ejercicio práctico.