Atracción gravitacional

Tal vez la historia de Newton y la manzana sea la más conocida sobre el desarrollo de una hipótesis científica. No es difícil imaginarse al físico inglés sentado al pie del manzano, con una hoja y una pluma, y describiendo la naturaleza de las cosas, cuando la descarada manzana cae sobre su peluca empolvada y le provoca el encendido de una vela (no había bombillas por entonces) que le hace ver con claridad el desarrollo teórico de la gravedad.

Sin duda, la historia debe de estar bastante edulcorada sobre la realidad, pero lo que sí pasó es que Isaac Newton (¿Brian May no será su reencarnación?) desarrolló el marco teórico para el tipo de fuerza que actúa sobre nosotros las 24 horas del día durante toda nuestra vida, incluso si nos convertimos en astronautas.

La gravedad se trata de una de las cuatro fuerzas fundamentales de la materia a la que hay que sumar el electromagnetismo, la fuerza nuclear fuerte (que da masa a la materia) y la fuerza nuclear débil (que produce la radioactividad). Es además la responsable de que el universo se encuentre en movimiento, atrayendo y repeliendo, satélites, planetas, estrellas, sistemas solares y galaxias.

En la Tierra la gravedad tiene una aceleración de 9.8 m/s2, que es la aceleración con la que es atraído un cuerpo de 1Kg de masa, pero esta aceleración no es igual en todos los puntos del planeta. El concepto de esfera no es real, ya que en realidad la Tierra se encuentra achatada por los poros, debido a la rotación, y su superficie no es homogénea, con altas montañas y profundas fosas oceánicas. Esto hace que haya una diferencia máxima de casi 20 Km entre el Everest y la fosa de las Marianas.

A pesar de estas diferencias no hay ningún punto en el que no exista gravedad. Con números grandes la gravedad continúa siendo de 9,8 en todo el planeta, pero existen una serie de condiciones que hacen que su cálculo definitivo tenga modificaciones en varios defínales.

Pero antes de todo, para poder comparar la gravedad sobre diferentes puntos hay que definir una superficie de referencia y esta se denomina geoide. El geoide es una esfera perfecta achatada en los poros, tal y como se podría representar al planeta, donde la circunferencia en el ecuador es mucho mayor que la circunferencia que pasa por ambos polos. La superficie que define este cuerpo es donde se debe definir la gravedad de un punto para poder compararlo con otros.

La morfología de la superficie de la Tierra hace que existan muy pocos puntos

que se encuentren exactamente sobre la superficie definida por el geoide, por lo tanto, cuando se mide la gravedad con gravímetro se está midiendo una gravedad relativa y lo que necesitamos es determinar la gravedad absoluta con respecto al geoide.

A la medida determinada es necesario realizarle una serie de correcciones siendo tres de ellas las más importantes, que puede añadir o restar aceleración a la medida.

La primera de ellas es la corrección de aire libre. Con ella se trata de eliminar la variable de la altura con respecto al geoide. Cuanto más alto se encuentre un punto sobre la superficie menor será la gravedad que le esté afectando. Esto es fácil de comprender al ver la fórmula básica de la gravedad la cual depende claramente de la distancia, donde a mayor distancia, menor atracción gravitacional.

Por lo que si el punto se encuentra por encima del geoide, es necesario sumarle una corrección, y si está por debajo, restársela.

La siguiente corrección es la de Bouguer, la cual está relacionada con la masa. Sin con la anomalía de aire libre se tenía en cuenta la altura, con esta corrección se tiene en cuenta la masa existente (o inexistente) entre la superficie real y la del geoide. Si hay más masa entonces la gravedad será mayor en el punto que midamos y todo lo contrario si hay inexistencia de esta.

La tercera corrección no se refiere a lo que sucede en el punto a medir sino con lo que se encuentra alrededor de este, es decir, a la topografía. La existencia de un relieve alrededor del punto supone que este ejerce una atracción y por lo tanto una reducción en la medida de que la gravedad que es necesario corregir.

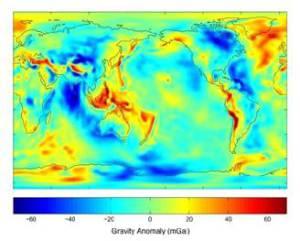
Con todas estas correcciones se puede finalmente formular un mapa donde todas las medidas se encuentran enrasadas a una misma superficie, la del geoide. En principio esto supondría una homogeneidad de los resultados, pero esto se encuentra muy alejado de la realidad. Principalmente por el principio de isostasia y segundo porque la corteza terrestre no es para nada homogénea y presenta zonas con densidades más altas y otras con más bajas.

Estos mapas de anomalías gravimétricas permite la exploración sobre todo en minería, donde por ejemplo, una anomalía muy alta puede ser el indicativo de una concentración anormal de hierro que podría ser explorada.