Botella de Klein… La “botella” que no tiene ni interior ni exterior

Botella de Klein

Traducción: “Centro de reciclado de botellas de Klein”

¿Qué es una botella de Klein?

Es un ejemplo de superficie (variedad topológica de dimensión 2) compacta (cerrada y acotada), conexa (de una pieza) y no orientable (contiene bandas de Möbius).

¿Eeeeehhhhnnnnn?

De acuerdo, vamos a dejarlo en que sería una “botella” que no tiene ni interior ni exterior, y tiene una sola cara. Digamos que se podría recorrer en su totalidad de forma continua, sin salto alguno.

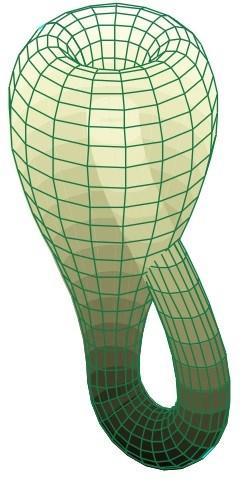
Representación bidimensional de la Botella de Klein inmersa en el espacio tridimensional. (Autor de la imagen: Tttrung. Licencia: CC BY-SA 3.0)

Por eso el señor de la VIÑETA que trabaja en el centro de reciclado de botellas de Klein que, como no puede ser de otra manera, funciona como una botella de Klein, ya no sabe si “entra”, “sale” o qué demonios está haciendo.

Fue descrita por primera vez en 1882 por el matemático alemán Felix Klein.

Al parecer, el nombre original del objeto no fue el de botella de Klein (en alemán Kleinsche Flasche), sino el de superficie de Klein (en alemán Kleinsche Fläche). El traductor de la primera referencia al objeto del alemán al inglés confundió las palabras. Como la apariencia de la representación tridimensional recuerda a una botella, casi nadie se dio cuenta del error. ^[1]

¿Cómo se construye una botella de Klein?

(Aviso que esto ya no es tan intuitivo, pero es muy interesante)

La botella de Klein es el cociente de un cuadrado cuyos lados están identificados como muestra la figura:

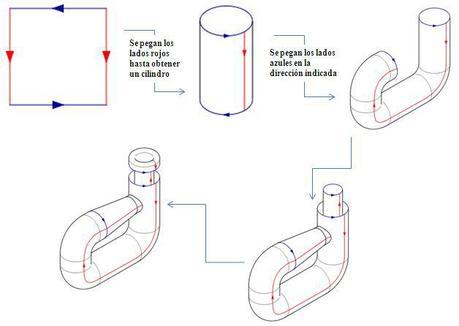
Botella de Klein como cociente de un cuadrado ^[2]

 Se puede ver también en esta animación:

Construcción de una botella de Klein (fuente)

Es importante tener en cuenta que, en realidad, la botella de Klein “no vive” en dimensión 3. En todas las representaciones de esta superficie, se autointerseca al realizar la identificación. Esta es la prueba de que no puede embeberse (incluirse de manera “fiel”) en el espacio en el que vivimos. La botella de Klein “vive” de manera natural en dimensión 4. ^[2]

Añadiendo una cuarta dimensión al espacio tridimensional, conseguimos que la botella pase a través de sí misma sin necesidad de un agujero. Para ello empujamos suavemente un trozo de tubo que contenga la intersección fuera del espacio tridimensional original. Una analogía útil es considerar una curva que se autointerseca en el plano; las intersecciones se pueden eliminar levantando una línea fuera del mismo. ^[1]

Bueno, ya avisé de que esto no iba a ser tan sencillo.

Y es que lo de la cuarta dimensión es algo que se escapa del alcanze de los mortales (me incluyo en ellos), por aquello de que no lo visualizamos.

Lo importante es quedarse con la idea de la peculiaridad de esta “botella”.

Con eso y con esto otro que se entiende bastante mejor y además es muy interesante:

Si seccionamos la botella de Klein en dos partes a lo largo de su plano de simetría resultan dos bandas de Möbius, cada una imagen especular de la otra (como si una de las bandas se mirase al espejo). Esto significa que, como en topología cortar es el proceso inverso a pegar, otra forma de construir una botella de Klein es pegando dos bandas de Möbius.

Pero además, si se corta por la línea roja de la imagen anterior (no se secciona completamente como antes), se obtiene una banda de Möbius. Lo cuál según acabamos de ver implica que, siguiendo el proceso inverso, se puede construir igualmente la botella de Klein apartir de una banda de Möbius.

Lo podéis visualizar mucho mejor con este vídeo hecho en la Universidad de Hannover…

Bueno, espero haber podido acercar al menos un poco esta curiosa superficie en forma de “botella” tan particular.

Viñeta de Mark Heath.

Fuentes consultadas:

^[1] Wikipedia. La enciclopedia libre (https://es.wikipedia.org/wiki/Botella_de_Klein)

^[2] Cuaderno de Cultura Científica (http://culturacientifica.com/2015/12/09/la-botella-de-klein-geometria-palindromica/)