Brevemáticas V: 1089

Escribe en un papel un número de 3 cifras, que no sea capicúa. Justo debajo, escribe el mismo número pero del revés (es decir, si has escrito el 752, pon debajo el 257). Ahora réstalos (si has sido tan listo como para no tener en cuenta cual de los 2 es mayor... toma el valor absoluto de dicha diferencia). Siguiendo con el ejemplo anterior, 752-257=495. Ahora debajo del resultado, vuelve a escribirlo... pero del revés (en nuestro ejemplo, como la diferencia era 495, escribimos debajo 594) Ah!, ojo, si te sale un número de 2 cifras, entendemos que la centena es 0 y la tenemos en cuenta. Ahora súmalos y verás como te ha salido... el mismo número del título del post: 1089.
Bueno, vamos a acudir a la típica frase: No lo llames magia, llámalo MATEMÁTICAS. Vamos a ver por qué funciona este pequeño truco, que a los más pequeños de las casas suele dejar alucinados.

Elijo un número de 3 cifras que no sea capicúa, es decir, tal que . Nuestro número, en realidad es . Si ahora lo escribimos del revés, tomaremos el número .
Vamos a restar estos dos número. Para ello, sin pérdida de generalidad, supondremos 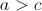c" style="display: inline;" alt="[;a>c;]" title="a>c" />, o lo que es lo mismo, el número mayor de los dos es el primero que hemos escrito y no el revertido (si fuese al revés, es decir, 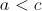, basta tener en cuenta que si revertimos el número revertido, volvemos a obtener el número original).
Al lío, restemos. . Pero ojo, que esto no quiere decir que el número elegido sea el que tiene por centenas a , por decenas al y por unidades al . No. Y la respuesta es que NO porque 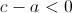<0" style="display: inline;" alt="[;c-a<0;]" title="c-a<0">. Así que veamos qué número es en realidad.

Muy sencillo, basta con ir llevándose de 1 en 1 para obtener una unidad positiva. Me explico:
.
Y ahora sí que podemos decir que el resultado es el que tiene por centenas a ,  por decenas al 9 y por unidades a .
Sigamos con el truco. Revirtamos el número: y sumémoslo al otro:

Y se acabó. Como veis, el resultado siempre sale 1089. Y el caso en que lo hemos salvado diciéndole a la persona a la que le hacemos el truco que tenga en cuenta el 0 de las centenas, si al hacer la diferencia le sale un número de 2 cifras.
Por cierto, si el número que tomamos como origen fuese capicúa, entonces el revertido coincide y la diferencia nos saldría 000... y el truco deja de funcionar. Por eso pedimos que no sea de este tipo. Otra posibilidad para hacérselo a varias personas, es decir que cada una de ellas piense un número del 0 al 9 diferente y formar un número con ellos y tomar ese como original.
Tito Eliatron Dixit
Referencias: Ruiz Domínguez, Xuxo (Mago Xuxo), Educando con magia.
PD: Esta entrada participa en la Edición 4.1231 del Carnaval de Matemáticas cuyo anfitrión es Matemáticas Interactivas y Manipulativas. 
 
Esta entrada se ha publicado originalmente en Tito Eliatron Dixit.
Si la estás viendo en otra web, probablemente estéás siendo víctima de un engaño.