Calculando la altura de un triangulo conocidos sus lados

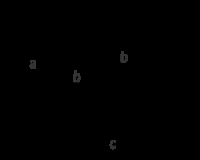
Hoy va la cosa de triángulos y la pregunta es sencilla. Dado un triángulo cualquiera ¿cómo calcularías (al menos) una de sus alturas? Vale, vamos a concretar algo más. Suponed que tenéis únicamente los lados de un triángulo y por supuesto, no disponéis de instrumentos de medida (ni reglas ni transportadores de ángulo ni nada que se le parezca). ¿Cómo calculáis una de sus alturas? Pensad un poco antes de continuar.
Yo os ofrezco, al menos, una solución.
Vamos a los casos sencillos. Si el triángulo es isósceles, la cosa es sencilla. Si llamamos a los 2 lados iguales y al otro lado (ojo, que en el caso de ser isósceles, y el argumento sigue siendo válido), resulta que la altura sobre el lado lo corta justo por la mitad:
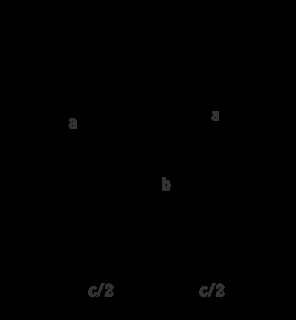Ahora basta aplicar el Teorema de Pitágoras para determinar que

Bien, pero... ¿qué ocurre si nuestro triángulo es escaleno? En este caso, cabe la remota posibilidad de que el triángulo sea rectángulo (por ejemplo, ) y así resulta que hay 2 alturas que coinciden con los lados y .
Pero, ¿qué pasa en general? ¿cómo podemos calcular una altura? O incluso en el caso de un triángulo (verdaderamente) isósceles, ¿cómo calculamos de forma sencilla la altura sobre uno de los lados iguales?
Aquí está el problema. Y mucho me temo que un alumno (medio) de secundaria hoy por hoy no sabría resolverlo. Y no lo haría por falta de una sencilla herramienta que no se suele explicar: La Fórmula de Herón.
La fórmula de Herón permite de forma relativamente sencilla calcular el área de un triángulo únicamente conocidos los lados (como es nuestro caso). Dicha fórmula, en su forma más simple, dice que:
 donde , es decir, el semiperímetro del triángulo.
Bien, una vez conocida la herramienta adecuada, ahora basta recordar la fórmula habitual del área del  triángulo para tener que
donde hemos denotado por   la altura correspondiente al lado .
¿Y a ti? ¿Se te ocurre otra manera de calcular una altura de un triángulo dados, exclusivamente, sus lados?
Tito Eliatron Dixit
PD: Esta entrada participa en la Edición 7.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.  
 
Esta entrada se ha publicado originalmente en Tito Eliatron Dixit.
Si la estás viendo en otra web, probablemente estéás siendo víctima de un engaño.