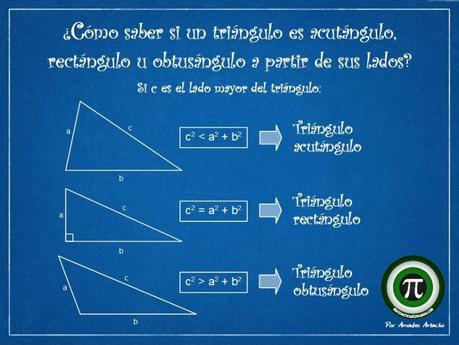
Vamos a ver un ejemplo.
Clasifica los siguientes triángulos en acutángulos, rectángulos u obtusángulos.
a) 25 cm, 24 cm, 7 cm.
b) 12 cm, 15 cm, 4 cm.
c) 2 cm, 12 cm, 12 cm.
Vamos con el primero.
El cuadrado del lado de mayor longitud (25 cm) es:
252 = 625Y la suma de los cuadrados de los otros dos lados (24 cm y 7 cm) es:
242 + 72 = 576 + 49 = 625Como podemos observar, el cuadrado del lado de mayor longitud es igual a la suma de los cuadrados de los otros dos lados del triángulo, luego se cumple el Teorema de Pitágoras y, por tanto, podemos afirmar que se trata de un triángulo rectángulo (tiene un ángulo de 90 grados).
Veamos ahora el segundo:
El cuadrado del lado de mayor longitud (15 cm) es:
152 = 225Y la suma de los cuadrados de los otros dos lados es:
122 + 42 = 144 + 16 = 160En este caso, el cuadrado del lado de mayor longitud es mayor que la suma de los cuadrados de los otros dos lados del triángulo, por lo que se trata de un triángulo obtusángulo (tiene uno de sus ángulos obtusos, es decir, mayor de 90 grados).
Vamos ahora con el tercero:
Hay dos lados cuya medida es la mayor (12 cm), es un triángulo isósceles, por lo que podemos considerar cualquiera de ellos como lado mayor.
El cuadrado del lado de mayor longitud (12 cm) es:
122 = 144Y la suma de los cuadrados de los otros dos lados es:
122 + 22 = 144 + 4 = 148El cuadrado del lado de mayor longitud es menor que la suma de los cuadrados de los otros dos lados y es, por tanto, un triángulo acutángulo (tiene sus tres ángulos agudos).
¿Te ha gustado? No te pierdas ninguna entrada del blog y suscríbete a los avisos por correo electrónico. Sabrás al instante cuándo se ha publicado una entrada nueva.
Únete a otros 3.545 suscriptores
Dirección de correo electrónico
La entrada ¿Cómo saber si un triángulo es acutángulo, rectángulo u obtusángulo a partir de sus lados? se publicó primero en MatematicasCercanas.
Puzzle Bobble
Karate Blazers
Puzzle De Bloques
Magical Cat Adventure