¿Cómo se obtiene la fórmula de las ecuaciones polinómicas de segundo grado?

Seguro que has resuelto más de una vez una ecuación polinómica de segundo grado de una variable, también conocida como ecuación cuadrática, cuya expresión general es:

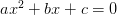
donde a, b y c son los coeficientes y x es la variable.

En la cual necesariamente a≠0, pues de lo contrario el primer término se anularía y ya no sería una ecuación de segundo grado.

Para hacerlo, habrás utilizado la famosa fórmula, que muy probablemente se habrá quedado grabada en tu cabeza, de…

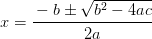
¡Bendita expresión que simplifica tanto las cosas!

Pero…

¿Sábes de dónde sale?

Pues vamos a verlo.

Para ello hacemos uso de los criterios de equivalencia de ecuaciones.

El primero de ellos dice que si a los dos miembros de una ecuación se les suma o se les resta una misma cantidad, la ecuación resultante es equivalente a la dada.

El segundo dice que si a los dos miembros de una ecuación se les multiplica o se les divide por una misma cantidad, la ecuación que se obtiene es equivalente a la de partida.

El que vamos a recorrer no es el único camino para llegar a nuestra famosa fórmula, pero sí es probablemente el más sencillo, y a mí me gustan las cosas sencillas.

Partimos de la expresión general de la ecuación polinómica de segundo grado:

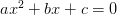
Restamos c a ambos lados…

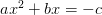
Multiplicamos ambos miembros por 4a…

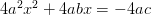
y sumamos b² en los dos lados…

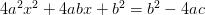
Alguien se preguntará que por qué hacemos todo esto. Pues bien, lo hacemos porque estamos buscando poder expresarlo como el cuadrado de un binomio, que es algo a lo que se recurre con bastante frecuencia en demostraciones matemáticas ya que suele simplificar mucho las cosas.

De hecho ese es el siguiente paso, porque el miembro de la izquierda se puede expresar como el cuadrado de un binomio:

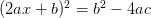
Ahora hacemos la raíz cuadrada a ambos lados…

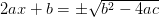
y restamos b en los dos miembros…

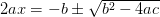
¡Casi lo tenemos!

Como se ve ya bastante claro, lo que nos queda por hacer es dividir a ambos lados por 2a…

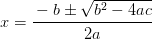
Et voilà!

Si esto fuese un GPS nos habría dicho: “Ha llegado a su destino”.

Como parece lógico, no hay por qué hacer todo esto para llegar a la expresión que nos da las soluciones de la ecuación cuadrática cada vez que tengamos que resolver una, pues para eso nos habremos aprendido la fórmula, para aplicarla directamente.

Pero al menos utilizarla no será ya un acto de fe y conoceremos su razón de ser.

Esta entrada participa en la Edición 7.7 del Carnaval de Matemáticas, que en esta ocasión organiza Los Matemáticos no son gente seria.