¿Cómo se obtiene la línea geodésica?

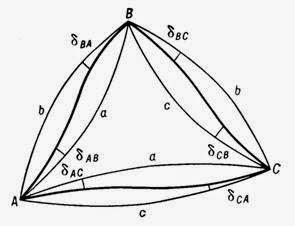
     En nuestro artículo anterior respondimos a la pregunta ¿qué es la línea geodésica? pero ¿les explicamos cómo se consigue? Ciertamente no, dejamos la puerta abierta al final del artículo y es hora de cerrar con broche de oro este interesante tópico.
     En arquitectura toda línea recta es una geodésica, sin embargo, también se acostumbra a desarrollar las superficies en planos para trazar una línea recta, que al ser llevada nuevamente la superficie a su forma original resulta siendo la geodésica.
    Zakatov en su curso de geodesia superior establece claramente los procedimientos a seguir para obtener la geodésica en una esfera, se definen así dos métodos: 
a) Primer método:
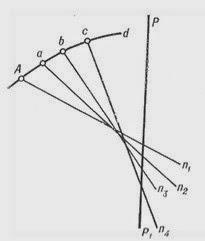•Sea P-P1 el eje menor del elipsoide
•A-n1 es la normal al elipsoide en el punto A.•Se estaciona el teodolito en el punto A.•En la dirección preestablecida se señala el punto a.•Se estaciona  el teodolito en a para hacer coincidir el instrumento con la normal a-n2. •Se visa al punto A, se gira la alidada 180º y se señala el punto b. •Se realiza nuevamente le procedimiento haciendo estación en b.

b) Segundo método:

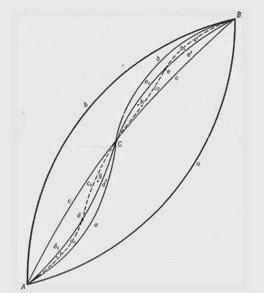
•AaB es la sección normal directa en el punto A.
•BbA es la sección normal directa en el punto B.•C es la intersección del elipsoide con la normal trazada por el centro la cuerda que una A y B.•Se traza un plano por A,C,B y que contenga a la normal en C, que genera la secciones AcCcB.•Se unen A, C y B mediante cuerdas.•Se trazan perpendiculares a ellas por su centro y generan los puntos d y e. •La sección directa desde A será Aa1d, la sección directa en B será Bb1e.
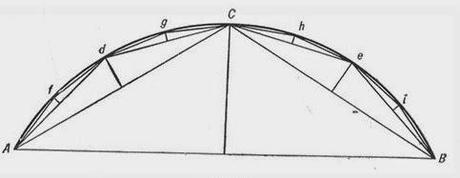
•Se unen los puntos A y d mediante una cuerda, se procede de igual forma para e y B.
•Se trazan perpendicular en el centro de las cuerdas para obtener los puntos f y g respectivamente.•Se unen los puntos nuevamente y se trazan perpendiculares. •Si se hace hasta el infinito se obtiene el plano de contacto.