Comparación de refuerzo (reinforcement comparison) para un problema Bandido Multibrazo (Multi-Armed Bandit)

Los métodos de comparación de refuerzo son similares a los métodos de seguimiento que vimos la semana pasada. En los que el bandido con el que se juega se selecciona en cada tirada aleatoriamente en base a unas probabilidades calculadas a partir de las recompensar empíricas.

Comparación de refuerzo

En el método de comparación de refuerzo el agente asigna una recompensa esperada a cada uno de los bandidos. La probabilidad de seleccionar a un bandido el siguiente episodio se calcula comparando la media empírica con la esperada, aumentando cuando la probabilidad esperada está por encima del promedio y disminuyendo cuando se encuentra por debajo. Siendo un método que funciona bien cuando los bandidos ofrecen valores de recompensa similares.

Este algoritmo parte de un valor que indica la preferencia de jugar con cada uno de los bandidos (\pi_i(t)). En cada uno de los episodios se calcula, a partir de estos valores, la probabilidad de jugar con cada uno de los bandidos utilizando la distribución de Boltzmann.

p_i(t) = \frac{e^{\pi_i(t)}}{\sum_j e^{\pi_j(t)}}

Una vez seleccionado el bandido y obtenida la recompensa se actualiza el valor de la preferencia para este. Lo que se hace mediante la siguiente expresión

\pi_i(t+1) = \pi_i(t) + \beta \left(r(t) + \bar{r}(t) \right)

donde \beta es un parámetro y \hat{r}(t) es el valor esperado de la recompensa en el episodio t que se actualiza mediante la siguiente expresión

\bar{r}(t+1) = (1 - \alpha) \bar{r}(t) - \alpha r(t)

en donde \alpha es otro parámetro.

Implementación en Python del método de comparación de refuerzo

Al igual que en ocasiones anteriores se puede reutilizar el código escrito para el método de valores iniciales optimistas. Lo que solamente nos obliga reescribir el método de selección ( select()) y actualizar el de ejecución para guardar después de cada ejecución ( run()). Así solamente se tiene que escribir la siguiente clase

class ReinforcementComparison(Epsilon):
    def __init__(self, bandits, alpha=0.001, beta=0.1):
        self.bandits = bandits
        self.alpha = alpha
        self.beta = beta
        
        self.reset()
       
    
    def run(self, episodes=1):
        for i in range(episodes):
            # Selección del bandido
            bandit = self.select()
            
            # Obtención de una nueva recompensa
            reward = bandits[bandit].pull()
            
            # Agregación de la recompensa al listado
            self._rewards.append(reward)
            
            # Actualización de la media
            self._plays[bandit] += 1
            self._mean[bandit] = (1 - 1.0/self._plays[bandit]) * self._mean[bandit] \
                                 + 1.0/self._plays[bandit] * reward
            
            # Actualización de la probablidad
            self._r[bandit] = (1 - self.alpha) * self._r[bandit] + self.alpha * reward
            self._pi[bandit] += self.beta * (reward - self._r[bandit])
    
        
        return self.average_reward()
    
    
    def select(self):
        # Calculo de la probabilidad de seleccionar un bandido
        prob = np.exp(self._pi)
        prob /= np.sum(prob)
        prob = np.cumsum(prob)
             
        # Selección del bandido
        return np.where(prob > np.random.random())[0][0] 
    
    
    def reset(self, initial=None):
        self._rewards = []
        self._plays = [0] * len(self.bandits)
        self._mean = [0] * len(self.bandits)
        
        self._pi = [0] * len(self.bandits)
        self._r = [0] * len(self.bandits)

En este caso se han creado dos propiedades privadas _pi y _r en las que se almacena el valor de preferencia y el valor de la recompensa esperada para cada uno de los bandidos. Valores que se actualizan al final del método run(). Al igual que en el caso de método de seguimiento, la selección del bandido con el que se juega en cada momento es aleatoria en base a las probabilidades asignadas a cada bandido.

Evaluación de los resultados

Una vez que ya tengamos la clase implementada se puede comparar el rendimiento de esta con UCB1. Usando para ello los bandidos basados en la distribución binomial que se usaron ya en otras ocasiones. Así se puede ejecutar el siguiente código para ver el rendimiento.

np.random.seed(0)

bandits = [Bandit(0.02), Bandit(0.06), Bandit(0.10)]

pursuit = ReinforcementComparison(bandits, alpha=0.001, beta=0.1)
ucb1 = UCB1(bandits)

pursuit.run(200000)
ucb1.run(200000)

pursuit.plot(True, label='Comparison')
ucb1.plot(True, True, label='UCB1')
plt.legend()

Obteniendo la siguiente figura.

Evolución de la recompensa promedio con el número de tiradas para el algoritmo de comparación de refuerzo (reinforcement comparison) y UCB1 con tres bandidos basados en una distribución binomial

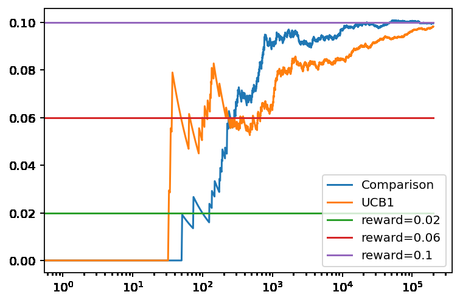
En esta figura se puede ver como el método de comparación de refuerzo ofrece una mayor recompensa promedio que UCB1 en ejemplo. La gráfica básicamente nos dice que el método de comparación identifica antes el bandido con mayor recompensa, en torno a los 200 episodios ya ha se acerca al valor teórico del mejor bandido, mientras que UCB1 requiere más episodios. Algo que se puede apreciar también en el número de veces que ha jugado cada uno con los bandidos que no son óptimos, 414 veces el método de comparación frente a las 12.573 de UCB1. Esto es, UCB1 ha seleccionado un bandido no óptimo en 30 más ocasiones.

Conclusiones

En esta entrada hemos visto un método sencillo para decidir qué bandido se selecciona en cada una de las tiradas en un problema tipo bandido multibrazo con el que se puede obtener mejores resultados que UCB1.

Imagen de Janusz Jeziorski en Pixabay