Publicado por Ezequiel L
¿Cómo puede un universo empezar con unos pocos tipos de partículas elementales en el big bang y acabar generando vida, literatura e incluso este blog? ¿por qué el big bang no acabó simplemente provocando una nube de polvo o un cristal gigante? Aquí entra en juego un concepto, llamado complejidad (mental o matemático, dependerá de cada uno).
El comportamiento complejo en la naturaleza refleja una tendencia de grandes sistemas con muchos componentes a evolucionar a estados ‘críticos‘, que lejos de ser ‘equilibrados’, es un punto en el que cualquier estímulo podría provocar una avalancha en todo el sistema (¿¿Nos suena de algo??).
La mayoría de los cambios en la naturaleza tienen lugar a través de eventos catastróficos y no por una evolución suave y gradual.
Este llamado estado crítico se establece por la interacciones incesantes entre cada uno de los individuos del conjunto: otro concepto para nuestro paladar, la auto-organización.
Aunque nos suene a sindicalismo, la criticalidad auto-organizada es el único mecanismo conocido para generar complejidad.
Seamos un poco más gráficos, imaginemos el típico niño aburrido ese día de Agosto en la playa, cogiendo un puñado de arena y dejándola caer para formar una pila grano a grano. Al principio, el montón de arena es casi plano y cada grano se queda cerca de donde cayó y su comportamiento puede entenderse con las leyes de la física aplicadas a cada grano. A medida que el montón empieza a hacerse cada vez más grande, van creciendo la pendiente en los laterales de la pila. Eventualmente, parte de la arena puede deslizarse por la pendiente o incluso casi toda la arena. En este punto, el sitema está lejos de un equilibrio y su comportamiento no puede entenderse a partir del comportamiento de los granos individuales. Las dinámicas de las avalanchas forman una dinámica en sí misma, cuando un sistema se comporta así, decimos que es COMPLEJO.
(Nos sigue sonando?)
de acuerdo con las leyes de la física. Una ley de Newton que nos dice como se mueve un objeto, una ley de Maxwell que nos dice como interacciona magnetismo y electricidad, etc. Pero por simple que sea la ecuación y la situación, la matemática se puede volver increíblemente difícil. Por ejemplo el movimiento de dos planetas en el campo gravitatorio del Sol y los demás planetas, podríamos dejarnos la mano haciéndolo. Afortunadamente hoy existen ordenadores a los que podemos engañar para que lo hagan por nosotros, como en la simulación que vemos en el vídeo. Alguien le pone leyes físicas a una nube de gas y venga, a correr unos billones de años (a cámara rápida).
Es por esto, que existen conceptos que nosotros conocemos muy bien como la presión y la temperatura, conceptos macroscópicos que nos reflejan estadísticamente qué pasa a nivel microscópico. Digamos que no sentimos átomo a átomo al tocar algo caliente, sino un promedio de sus movimientos en conjunto. ¿Esto es muy profundo verdad?
Bueno, a donde iba, el objetivo científico de introducir una teoría de complejidad es predecir, pero me temo que aún estamos en la frontera del estudio a posteriori de este comportamiento. Eso no nos impide disfrutar iluminándonos con sus manisfetaciones.
Por ejemplo los terremotos, ¿parece algo como la pila de arena no?, hay unos movimientos tectónicos, unos elementos que interaccionan, una especie de acumulación de presión y la avalancha, el terremoto. La escala de Richter no es ningún capricho, surge a partir de la observación de que por cada 1000 terremotos de magnitud 4, habrá 5 de magnitud 100 , 10 de magnitud 6,…
Representando esto en escala logarítmica (ponemos en un eje 10,100,1000,… en lugar de 1,2,3,…)
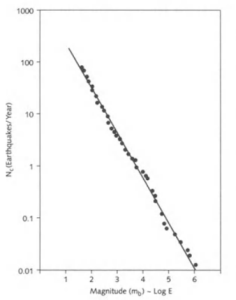
Y aquí lo impresionante, cómo algo que tiene tantas variables como un terremoto, millones de elementos que interaccionan entre sí como piezas de dominó, resultan en algo tan bello y simple.
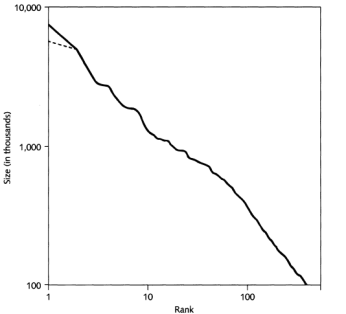
A los más peseteros se les estará pasando por la cabeza “¡¡La Bolsa!!”, pues sí, se han estudiado variaciones de precios, por ejemplo el precio del algodón, este ejemplo es de 1963
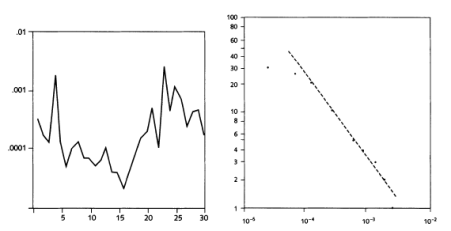
La gráfica de la izquierda muestra la variación del precio por mes y la de la derecha el número de veces que se supera cierto valor. Sin embargo, como ya he dicho, al ser estudio a posteriori, nadie puede hacerse rico sólo conociendo esto, ohhhhhh lástima… Qué va..
Si alguna vez has ido en un avión y te has preguntado cuánto mide la longitud de una costa con entrantes y salientes y que cuanto más afines la medida, más salientes habrá que medir, no has sido el primero, pero tienes una mente privilegiada y te gustará lo que hizo Mandelbrot, que definió este comportamiento como fractal.
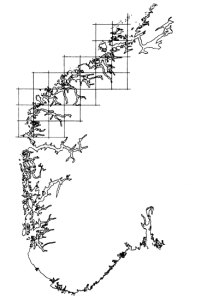
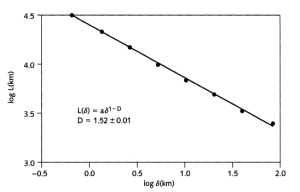
Aquí podemos ver la costa de Noruega con sus fiordos y qué ocurre si representamos la longitud de costa obtenida en función del número de cajas de tamaño d para cubrirla, pues volvemos a obtener una maravillosa ley de potencias. El tema de los fractales es impresionante y muy amplio, volveremos sobre él en este blog.
Por último veamos un par de ejemplos curiosos más. Y si normalmente, de nuestro comportamiento emergen también este tipo de leyes. La respuesta:
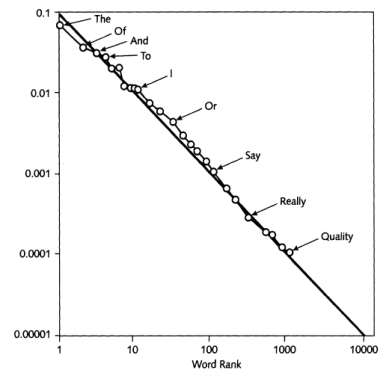
La lista de fenómenos es larga, wikipedia nos da una idea:
- The frequency-dependency of acoustic attenuation in complex media
- The Stevens’ power law of psychophysics
- The Stefan–Boltzmann law
- The input-voltage–output-current curves of field-effect transistors and vacuum tubes approximate a square-law relationship, a factor in “tube sound“.
- Square-cube law (ratio of surface area to volume)
- Kleiber’s law relating animal metabolism to size, and allometric laws in general
- A 3/2-power law can be found in the plate characteristic curves of triodes.
- The inverse-square laws of Newtonian gravity and electrostatics, as evidenced by the gravitational potential and Electrostatic potential, respectively.
- Self-organized criticality with a critical point as an attractor
- Exponential growth and random observation (or killing)[13]
- Progress through exponential growth and exponential diffusion of innovations[14]
- Highly optimized tolerance
- Model of van der Waals force
- Force and potential in simple harmonic motion
- Kepler’s third law
- The initial mass function of stars
- The M-sigma relation
- Gamma correction relating light intensity with voltage
- The two-thirds power law, relating speed to curvature in the human motor system.
- The Taylor’s law relating mean population size and variance of populations sizes in ecology
- Behaviour near second-order phase transitions involving critical exponents
- Proposed form of experience curve effects
- The differential energy spectrum of cosmic-ray nuclei
- Fractals
- Pareto distribution and the Pareto principle also called the “80–20 rule”
- Zipf’s law in corpus analysis and population distributions amongst others, where frequency of an item or event is inversely proportional to its frequency rank (i.e. the second most frequent item/event occurs half as often the most frequent item, the third most frequent item/event occurs one third as often as the most frequent item, and so on).
- The safe operating area relating to maximum simultaneous current and voltage in power semiconductors.
- Supercritical state of matter and supercritical fluids, such as supercritical exponents of heat capacity and viscosity.[15]
- Zeta distribution (discrete)
- Yule–Simon distribution (discrete)
- Student’s t-distribution (continuous), of which the Cauchy distribution is a special case
- Lotka’s law
- The scale-free network model
- Pink noise
- Neuronal avalanches[3]
- The law of stream numbers, and the law of stream lengths (Horton‘s laws describing river systems)[citation needed]
- Populations of cities (Gibrat’s law)[citation needed]
- Bibliograms, and frequencies of words in a text (Zipf’s law)[citation needed]
- 90–9–1 principle on wikis (also referred to as the 1% Rule)[citation needed]
- Richardson’s Law for the severity of violent conflicts (wars and terrorism){Lewis Fry Richardson, The Statistics of Deadly Quarrels, 1950}
- Gutenberg–Richter law of earthquake magnitudes
- Social Network Websites
Iremos pasando por algunos de estos temas, de manera más o menos interesante y os animo a que indaguéis e imaginéis vosotros también.
Referencias:
- How nature works?- Per Bak
- http://en.wikipedia.org/wiki/Power_law


