Las cónicas aparecen espontáneamente en la naturaleza y, por sus propiedades y su belleza, son muy utilizadas en la astronomía, en la arquitectura y en la física. ¿Quieres ver algunos ejemplos que demuestran esto?
Órbitas de planetas y cometas
Cuando en el siglo III a.C., Apolonio descubrió las tres cónicas fundamentales, estaba muy lejos de imaginarse que dichas curvas se ajustaban a los movimientos de los cuerpos celestes. A este notable matemático le debemos estos nombres: elipse, parábola e hipérbola.
Durante muchos siglos se consideró que las órbitas de los planetas eran circulares. Fue a comienzos del siglo XVII cuando Kepler enunció sus importantes leyes, que asignan órbitas elípticas a dichos cuerpos. La vida en la tierra depende de una elipse!
¿Qué pasó un siglo antes?
Que Copérnico dio al traste con la concepción geocéntrica del Universo, intentando hacer ver a los incrédulos que era la Tierra la que giraba alrededor del Sol.
Los cometas también tienen órbitas elípticas alargadas e incluso algunos de ellos, tienen órbitas hiperbólicas.
¿Cómo puedes obtener las cónicas?
Es bastante sencillo. Puedes verlo bien en el siguiente esquema. Si “cortas un doble cono” por diversos planos, según su inclinación, las intersecciones que se producen dan lugar a curvas bien definidas: las cónicas. En este caso te presento las 4 posibilidades que se pueden producir cuando el plano no pasa por el vértice.
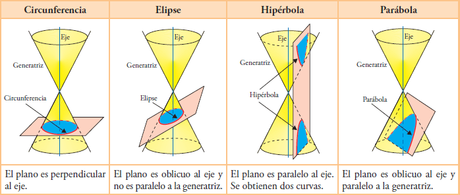
Haz clic aquí si quieres verlo en un vídeo con más detalle. ¿Quieres construir tus propias cónicas a partir de un doble cono? Pulsa
Importancia de las cónicas
Las órbitas de los cuerpos celestes, las antenas de satélites, los faros de los coches, las bóvedas, etc. son lugares donde aparecen diferentes cónicas.
Todos los días “dibujas” elipses cuando bebes agua en un vaso. Porque lo inclinas, ¿verdad?. Si juegas al baloncesto te gustarán mucho las parábolas.
Y en la estación de metro ¿por qué se oyen las conversaciones de algunas personas que están en el otro andén como si estuviesen al lado tuyo? Porque el que habla y el que escucha están cerca de los focos de una elipse.
Cómo dibujar una elipse
Pregúntale a un jardinero, él te dará la respuesta… (jeje)
Los que tienen las suerte de trabajar en un jardín con plantas (me encantan) puede que alguna vez hayan utilizado este método para trazar un parterre de forma elíptica: se clavan en el suelo dos estacas, se ata entre ambas una cuerda suficientemente amplia y se procede como en esta imagen animada. Tú también puedes hacerlo en casa con dos chinchetas y con un hilo fuerte.

Elipse, la cónica “más sencilla”
¿No tienes chinchetas? No importa, con Geogebra también lo puedes hacer. Puedes dibujar fácilmente una elipse haciendo clic aquí. No me cansaré de recomendar el uso de estas herramientas.
Observa que belleza, una curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría y con un ángulo mayor que el de la generatriz respecto del eje de revolución.
La elipse también es un caso particular de hipotrocoide, donde R = 2r, siendo R el radio de la circunferencia directriz, y r el radio de la circunferencia generatriz.
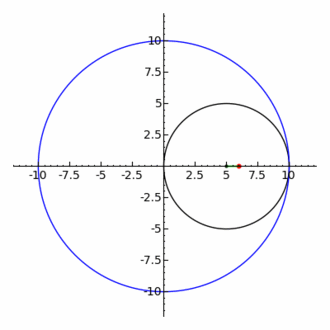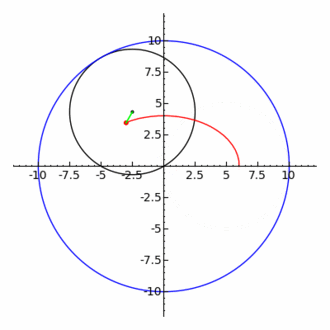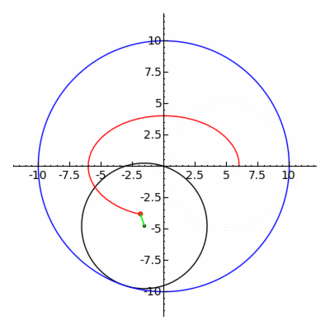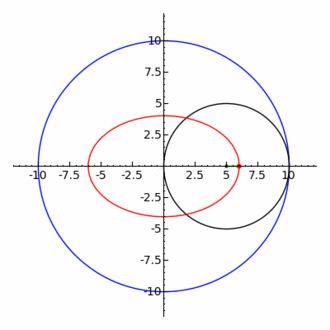
En una curva hipotrocoide (menuda palabreja!), la circunferencia que contiene al punto generatriz, gira tangencialmente por el interior de la circunferencia directriz. (si, es bastante lioso lo reconozco)
Cómo dibujar una parábola
Esta curva ya no es tan sencilla de dibujar. Este vídeo explica bastante bien cómo trazar una parábola por puntos. Espero que te sea útil.
Aquí resulta mucho más sencillo imaginarse la parábola. Tira una pelota o un papel arrugado hacia adelante con un poco de fuerza. Ya la tienes! Cualquier objeto lanzado al aire de forma horizontal u oblicua realiza una parábola bajo la acción de la gravedad.Otro ejemplo son los vistosos arcos parabólicos creados por las fuentes de las ciudades.
Cómo dibujar una hipérbola
Se pueden obtener los puntos de la hipérbola con regla y compás. También es un procedimiento laborioso.
La hipérbola es la cónica menos habitual, pero también la podemos encontrar en la vida cotidiana. Los diseños de microscopios usan hipérbolas. Las señales de los sistemas de radio emplean funciones hiperbólicas. Usando las hipérbolas, los astrónomos pueden predecir el camino del satélite para hacer ajustes de forma que el satélite llegue a su camino.También la encontrarás en la física. ¿Te suena por ejemplo la ley de Boyle-Mariotte?
Lugares geométricos
Un lugar geométrico es el conjunto de todos los puntos que cumplen una cierta propiedad.
Las cónicas son lugares geométricos con ecuaciones bien definidas. Seguro que te puedes atrever a dar una definición de la circunferencia como lugar geométrico. No me quiero extender demasiado, pero para que te hagas una idea te dejo un breve resumen.
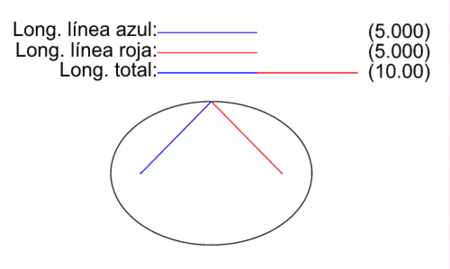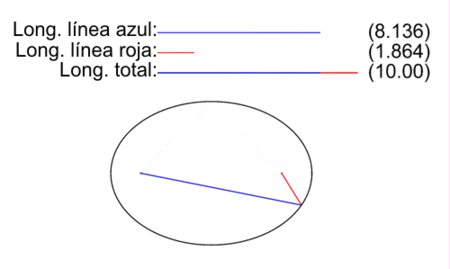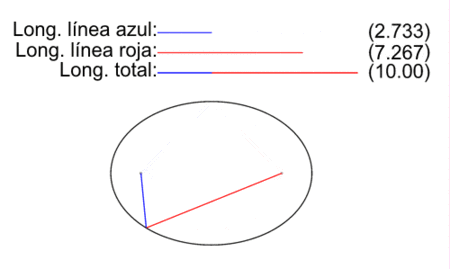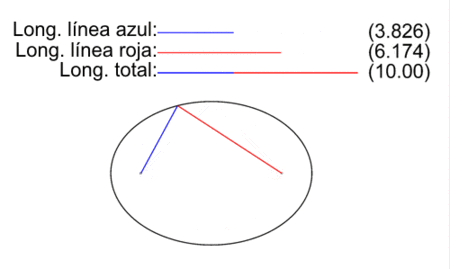
Elipse: lugar geométrico de los puntos P, cuya suma de distancias a dos puntos fijos (los focos F y F’) es una constante k
distancia (P, F) + distancia (P, F’) =k
Con este gif animado puedes comprobar que en todo momento se cumple esta igualdad. Recuerda, puedes hacerlo con chinchetas!
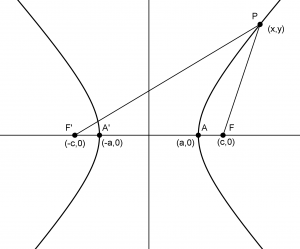
Hipérbola: lugar geométrico de los puntos P, cuya diferencia de distancias a dos puntos fijos (los focos F y F’) es una constante k
|distancia (P, F) – distancia (P, F’)|=k
Parábola: lugar geométrico de los puntos P que equidistan de un foco F y de una recta d llamada directriz
distancia (P,F) = distancia (P,d)


