Tenemos las dos raíces siguientes… ¿Cuál es mayor?
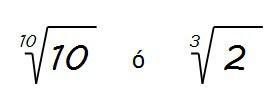
Una pista: La diferencia entre ambas es menor de 0,001.
¡Quieta esa calculadora!
Vamos a pensar un poco y verlo sin calculadora, que para eso son las matemáticas… para pensar.
Como la diferencia es tan pequeña, necesitamos algún tipo de lupa matemática que nos permita amplificarla y, así, hacerla visible…
Como en ambos casos el resultado de la raíz es mayor de la unidad, si hay algo en matemáticas que nos permite amplificar las cosas son las potencias.
Así que vamos a elevar cada número a la 30ª potencia…
No es casualidad haber escogido 30 como exponente. Si os fijáis 30 es el mínimo común múltiplo (m.c.m.) de 10 y 3 (los índices de las raíces). En breve veremos la razón de elevarlos a 30.
Esto podemos escribirlo de la siguiente manera…
Ahora agrupamos los de la izquierda de diez en diez y los de la derecha de tres en tres…
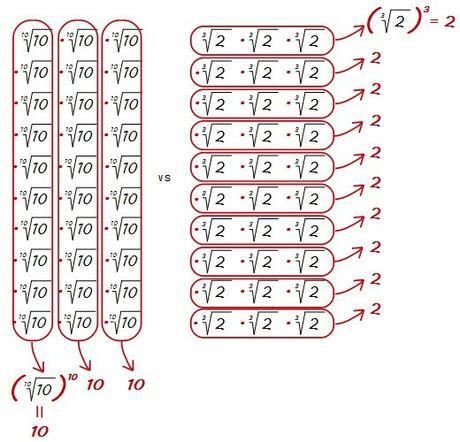
Y de esta manera ahora es más fácil hacer la comparación…
Así que podemos decir que:
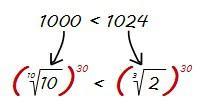
Y, por tanto:
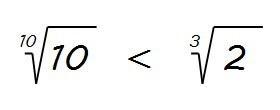
Ahora sí, podemos comprobarlo con la calculadora (seguro que hay personas que no se habían resistido a hacerlo)…
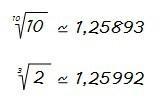
Pues, como veis, es interesante esto de tener una lupa matemática que nos permita amplificar las cosas para verlas mejor.
Y lo mejor de todo es que podemos buscar la lupa que necesitemos para cada situación…
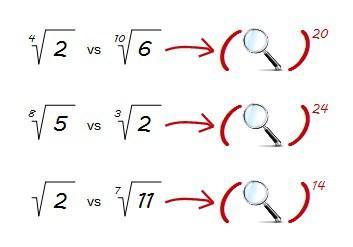
… basta con considerar, según habíamos visto, como exponente el m.c.m. de los índices de las raíces.
¡Os animo a que probéis!
Idea original: visto en Math with bad drawings
Las imágenes utilizadas en la entrada son de autoría propia
Puzzle Bobble
Karate Blazers
Puzzle De Bloques
Magical Cat Adventure